
【题目】某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:
f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(1)求实验室这一天的最大温差;
(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
【答案】
(1)解:∵f(t)=10﹣ ![]() =10﹣2sin(
=10﹣2sin( ![]() t+
t+ ![]() ),t∈[0,24),
),t∈[0,24),
∴ ![]() ≤
≤ ![]() t+
t+ ![]() <
< ![]() ,故当
,故当 ![]() t+
t+ ![]() =
= ![]() 时,及t=14时,函数取得最大值为10+2=12,
时,及t=14时,函数取得最大值为10+2=12,
当 ![]() t+
t+ ![]() =
= ![]() 时,即t=2时,函数取得最小值为10﹣2=8,
时,即t=2时,函数取得最小值为10﹣2=8,
故实验室这一天的最大温差为12﹣8=4℃.
(2)解:由题意可得,当f(t)>11时,需要降温,由(Ⅰ)可得f(t)=10﹣2sin( ![]() t+
t+ ![]() ),
),
由10﹣2sin( ![]() t+
t+ ![]() )>11,求得sin(
)>11,求得sin( ![]() t+
t+ ![]() )<﹣
)<﹣ ![]() ,即
,即 ![]() <
< ![]() t+
t+ ![]() <
< ![]() ,
,
解得10<t<18,即在10时到18时,需要降温.
【解析】(1)利用两角和差的正弦公式化简函数解析式为f(t)10﹣2sin( ![]() t+
t+ ![]() ),t∈[0,24),利用正弦函数的定义域和值域求得f(x)的最大值及最小值,可得实验室这一天的最大温差.(2)由题意可得,当f(t)>11时,需要降温,由f(t)>11,求得sin(
),t∈[0,24),利用正弦函数的定义域和值域求得f(x)的最大值及最小值,可得实验室这一天的最大温差.(2)由题意可得,当f(t)>11时,需要降温,由f(t)>11,求得sin( ![]() t+
t+ ![]() )<﹣
)<﹣ ![]() ,即
,即 ![]() <
< ![]() t+
t+ ![]() <
< ![]() ,解得t的范围,可得结论.
,解得t的范围,可得结论.
【考点精析】掌握函数y=Asin(ωx+φ)的图象变换是解答本题的根本,需要知道图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】教材上一例问题如下:
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
某同学利用图形计算器研究它时,先作出散点图(如图所示),发现两个变量不呈线性相关关系. 根据已有的函数知识,发现样本点分布在某一条指数型曲线![]() 的附近(
的附近(![]() 和
和![]() 是待定的参数),于是进行了如下的计算:
是待定的参数),于是进行了如下的计算:
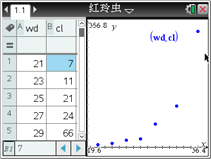
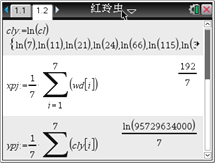
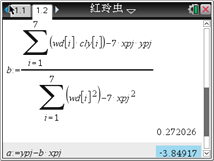
根据以上计算结果,可以得到红铃虫的产卵数y对温度x的回归方程为__________.(精确到0.0001) (提示:![]() 利用代换可转化为线性关系)
利用代换可转化为线性关系)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1的所有棱长都相等,AC∩BD=O, 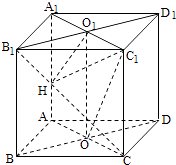 A1C1∩B1D1=O1 , 四边形ACC1A1和四边形BDD1B1均为矩形.
A1C1∩B1D1=O1 , 四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1﹣OB1﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)满足 ![]() f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
①f(x)=sin ![]() x,g(x)=cos
x,g(x)=cos ![]() x;
x;
②f(x)=x+1,g(x)=x﹣1;
③f(x)=x,g(x)=x2 ,
其中为区间[﹣1,1]上的正交函数的组数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)= ![]() (|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
(|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的函数,如果存在常数
上的函数,如果存在常数![]() ,对区间
,对区间![]() 的任意划分:
的任意划分:![]() ,和式
,和式![]() 恒成立,则称
恒成立,则称![]() 为
为![]() 上的“绝对差有界函数”,注:
上的“绝对差有界函数”,注:![]() .
.
(1)求证:函数![]() 在
在![]() 上是“绝对差有界函数”;
上是“绝对差有界函数”;
(2)记集合![]() 存在常数
存在常数![]() ,对任意的
,对任意的![]() ,有
,有![]() 成立.
成立.
求证:集合![]() 中的任意函数
中的任意函数![]() 为“绝对差有界函数”;
为“绝对差有界函数”;
(3)求证:函数 不是
不是![]() 上的“绝对差有界函数”.
上的“绝对差有界函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0 , 且x0>0,则实数a的取值范围是( )
A.(1,+∞)
B.(2,+∞)
C.(﹣∞,﹣1)
D.(﹣∞,﹣2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数![]() 满足
满足![]() ,定义域为
,定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在
在![]() 上有零点,求
上有零点,求![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com