
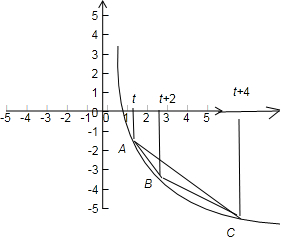
 x的图象上(如图),有A、B、C三点,它们的横坐标依次为t、t+2、t+4,其中t≥1,
x的图象上(如图),有A、B、C三点,它们的横坐标依次为t、t+2、t+4,其中t≥1,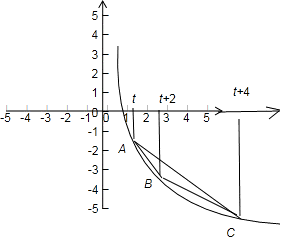
 t),(t+2,log
t),(t+2,log (t+2)),(t+4,log
(t+2)),(t+4,log (t+4)),由图形,当妨令三点A,B,C在x轴上的垂足为E,F,N,则△ABC的面积为
(t+4)),由图形,当妨令三点A,B,C在x轴上的垂足为E,F,N,则△ABC的面积为 t+log
t+log (t+2)]+[log
(t+2)]+[log (t+2)+log
(t+2)+log (t+4))]+2[log
(t+4))]+2[log t-log
t-log (t+4))]
(t+4))] t+log
t+log (t+4)-2log
(t+4)-2log (t+2)]=
(t+2)]= =
=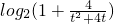
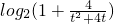 (t≥1)
(t≥1)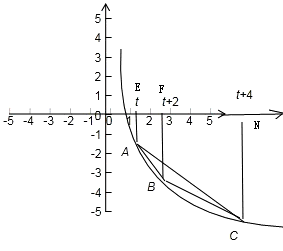
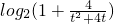 (t≥1)是复合函数,其外层是一个递增的函数,t≥1时,内层是一个递减的函数,故复合函数是一个减函数,
(t≥1)是复合函数,其外层是一个递增的函数,t≥1时,内层是一个递减的函数,故复合函数是一个减函数,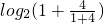 =
=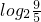
 t),(t+2,log
t),(t+2,log (t+2)),(t+4,log
(t+2)),(t+4,log (t+4)),
(t+4)),

科目:高中数学 来源: 题型:
 在对数函数y=log
在对数函数y=log | 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.a>-2 | B.a<-1 | C.-2<a<-1 | D.a>-1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省广州市荔湾区新会一中高一(上)期中数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com