练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在底面半径为3，高为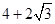的圆柱形有盖容器中，放入一个半径为3的大球后再放入与球面、圆柱侧面及上底面均相切的小球，则放入的小球的个数最多的为

    A．4个B．5个C．6个D．7个

    C

    解析试题分析：因为在底面半径为3，高为的圆柱形有盖容器中，放入一个半径为3的大球后其与底面和侧面都相切，那么通过作出截面图可知，如果再放入与球面、圆柱侧面及上底面均相切的小球，则放入的小球的个数最多的为6个，并且是对称放置的，左边和右边各有3个，因此选C.
    考点：球体与圆柱体的结合体
    点评：解决的关键是明白弄清楚球与球相切时，以及球与柱体的面相切时，放入的球的个数最多，属于中档题。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    点A、B、C、D在同一个球的球面上，AB=BC= , AC=2,若四面体ABCD体积的最大值为，则这个球的表面积为
    A．           B．            C．             D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图是某简单组合体的三视图，则该组合体的体积为（     ）  
     

    A． B．
    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    将长方体截去一个四棱锥得到的几何体如图所示，则该几何体的侧视图为

                  
    A．        B．       C．       D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图是一个空间几何体的正视图、侧视图、俯视图，如果正视图、侧视图所对应的三角形皆为边长为2的正三角形，俯视图对应的四边形为正方形，那么这个几何体的体积为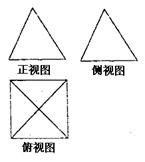

    A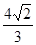． B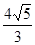． C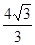． D．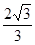

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    正四面体ABCD(六条棱长都相等)的棱长为1，棱AB∥平面，则正四面体上的所有点在平面内的射影构成的图形面积的取值范围是（   ）

    A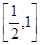．B．C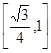．D．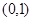

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若正方体的棱长为，则以该正方体各个面的中心为顶点的凸多面体的体积为 （   ）

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某几何体的直观图如右图所示，则该几何体的侧（左）视图的面积为（ ）

    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知三棱锥的底面是边长为的正三角形，其正视图与俯视图如图所示，则其侧视图的面积为

    A． B． C． D． 

    查看答案和解析>>

    同步练习册答案