
【题目】![]() 是自然对数的底数,
是自然对数的底数,![]() ,已知函数
,已知函数![]() ,
,![]() .
.
(1)若函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围;
的取值范围;
(2)对于![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)函数![]() 有零点等价于对应方程有实数解,进而分离参数,并通过构造函数
有零点等价于对应方程有实数解,进而分离参数,并通过构造函数![]() ,结合求导,利用函数的单调性来确定其最值,从而得以确定参数
,结合求导,利用函数的单调性来确定其最值,从而得以确定参数![]() 的范围;(2)通过所要证明的不等式的等价转化,转化为两个不等式问题,通过分类讨论分别加以证明,构造函数并求导,结合函数的单调性与最值来证明与转化.
的范围;(2)通过所要证明的不等式的等价转化,转化为两个不等式问题,通过分类讨论分别加以证明,构造函数并求导,结合函数的单调性与最值来证明与转化.
(1)由函数![]() 有零点知,方程
有零点知,方程![]() 有实数解,因为
有实数解,因为![]() ,所以
,所以![]() .设
.设![]() ,
,![]() ,
,
则![]() 的取值范围转化为函数
的取值范围转化为函数![]() 在
在![]() 上的值域.
上的值域.
因为![]() ,所以当
,所以当![]() ,
,![]() 时
时![]() ,函数
,函数![]() 在
在![]() 上单调递增,当
上单调递增,当![]()
![]() 时
时![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
故函数![]() 在
在![]() 时,取得最大值
时,取得最大值![]() ,
,
又![]() 上,
上,![]() ,所以函数
,所以函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,![]() .当
.当![]()
![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,![]() .
.
从而函数![]() 有零点时,实数
有零点时,实数![]() 的取值范围为
的取值范围为![]() ,
,![]()
(2)![]() 可以转化为证明两个不等式
可以转化为证明两个不等式![]()
![]()
![]() ①,
①,![]() ②.
②.
设![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,
时,
![]() ,函数
,函数![]() 在
在![]() 上单调递增.故函数
上单调递增.故函数![]() 在
在![]() 时,取得最小值
时,取得最小值
![]() ,所以
,所以![]() .
.
得证![]() ①
①
设![]() ,有
,有![]() ,当
,当![]() 时,
时,![]() .函数
.函数![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,函数
时,函数![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
故函数![]() 在
在![]() 时,取得最小值
时,取得最小值![]() .
.
所以![]() ,得
,得![]() .(仅当
.(仅当![]() 时取等号)
时取等号)
又由![]() 为增函数,得
为增函数,得![]() ②.
②.
合并①②得证![]() .
.


科目:高中数学 来源: 题型:
【题目】法国的数学家费马(PierredeFermat)曾在一本数学书的空白处写下一个看起来很简单的猜想:当整数![]() 时,找不到满足
时,找不到满足![]() 的正整数解.该定理史称费马最后定理,也被称为费马大定理.费马只是留下这个叙述并且说他已经发现这个定理的证明妙法,只是书页的空白处不够无法写下.费马也因此为数学界留下了一个千古的难题,历经数代数学家们的努力,这个难题直到1993年才由我国的数学家毛桂成完美解决,最终证明了费马大定理的正确性.现任取
的正整数解.该定理史称费马最后定理,也被称为费马大定理.费马只是留下这个叙述并且说他已经发现这个定理的证明妙法,只是书页的空白处不够无法写下.费马也因此为数学界留下了一个千古的难题,历经数代数学家们的努力,这个难题直到1993年才由我国的数学家毛桂成完美解决,最终证明了费马大定理的正确性.现任取![]() ,则等式
,则等式![]() 成立的概率为( )
成立的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角系![]() 中,点A为曲线C:
中,点A为曲线C:![]() 在第一象限的图象上的动点,点E,G在曲线C的准线
在第一象限的图象上的动点,点E,G在曲线C的准线![]() 上,且点G在x轴的下方,圆O与准线相切,直线
上,且点G在x轴的下方,圆O与准线相切,直线![]() 交曲线C于点B,交圆O于点D,H.
交曲线C于点B,交圆O于点D,H.
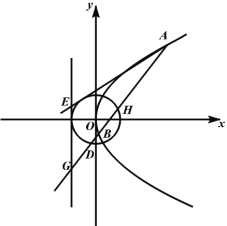
(1)当点H为曲线C的焦点,![]() 时,求
时,求![]() ;
;
(2)当点O为![]() 的内心时,若
的内心时,若![]() ,求点A的坐标.
,求点A的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的两切线,切点为
的两切线,切点为![]() .
.
(1)求两切点![]() 所在的直线方程;
所在的直线方程;
(2)椭圆![]() ,离心率为
,离心率为![]() ,(1)中直线AB与椭圆交于点P,Q,直线
,(1)中直线AB与椭圆交于点P,Q,直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是空气质量的一个重要指标,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35μg/m3以下空气质量为一级,在35μg/m3~75μg/m3之间空气质量为二级,在75μg/m3以上空气质量为超标.如图是某市2019年12月1日到10日PM2.5日均值(单位:μg/m3)的统计数据,则下列叙述不正确的是( )
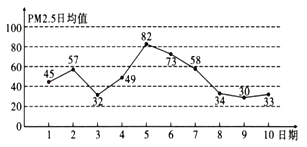
A.这10天中,12月5日的空气质量超标
B.这10天中有5天空气质量为二级
C.从5日到10日,PM2.5日均值逐渐降低
D.这10天的PM2.5日均值的中位数是47
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】地球的公转轨道可以看作是以太阳为一个焦点的椭圆,根据开普勒行星运动第二定律,可知太阳和地球的连线在相等的时间内扫过相等的面积,某同学结合物理和地理知识得到以下结论:①地球到太阳的距离取得最小值和最大值时,地球分别位于图中![]() 点和
点和![]() 点;②已知地球公转轨道的长半轴长约为
点;②已知地球公转轨道的长半轴长约为![]() 千米,短半轴长约为
千米,短半轴长约为![]() 千米,则该椭圆的离心率约为
千米,则该椭圆的离心率约为![]() .因此该椭圆近似于圆形:③已知我国每逢春分(
.因此该椭圆近似于圆形:③已知我国每逢春分(![]() 月
月![]() 日前后)和秋分(
日前后)和秋分(![]() 月
月![]() 日前后),地球会分别运行至图中
日前后),地球会分别运行至图中![]() 点和
点和![]() 点,则由此可知我国每年的夏半年(春分至秋分)比冬半年(当年秋分至次年春分)要少几天.以上结论正确的是( )
点,则由此可知我国每年的夏半年(春分至秋分)比冬半年(当年秋分至次年春分)要少几天.以上结论正确的是( )
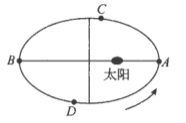
A.①B.①②C.②③D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com