练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】PM2.5是空气质量的一个重要指标，我国PM2.5标准采用世卫组织设定的最宽限值，即PM2.5日均值在35μg/m3以下空气质量为一级，在35μg/m3～75μg/m3之间空气质量为二级，在75μg/m3以上空气质量为超标.如图是某市2019年12月1日到10日PM2.5日均值（单位：μg/m3）的统计数据，则下列叙述不正确的是（ ）

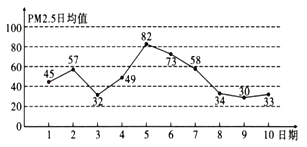
    A.这10天中，12月5日的空气质量超标

    B.这10天中有5天空气质量为二级

    C.从5日到10日，PM2.5日均值逐渐降低

    D.这10天的PM2.5日均值的中位数是47

    【答案】C

    【解析】

    先对图表信息进行分析，再由频率分布折线图逐一检验即可得解.

    解：由图表可知，选项A，B，D正确，

    对于选项C，由于10日的PM2.5日均值大于9日的PM2.5日均值，

    故C错误，

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆与抛物线有共同的焦点，且两曲线的公共点到的距离是它到直线 （点在此直线右侧）的距离的一半.

    （1）求椭圆的方程；

    （2）设为坐标原点，直线过点且与椭圆交于两点，以为邻边作平行四边形.是否存在直线，使点落在椭圆或抛物线上？若存在，求出点坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，已知菱形的对角线交于点，点为线段的中点，，，将三角形沿线段折起到的位置，，如图2所示．

    （Ⅰ）证明：平面 平面；

    （Ⅱ）求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面，，，且，，

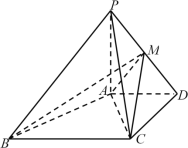
    （1）求证：；

    （2）在线段上，是否存在一点，使得二面角的大小为，如果存在，求与平面所成的角的正弦值，如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《周髀算经》是我国古老的天文学和数学著作，其书中记载：一年有二十四个节气，每个节气晷长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测影子的长度），夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降是连续的九个节气，其晷长依次成等差数列，经记录测算，这九个节气的所有晷长之和为49.5尺，夏至、大暑、处暑三个节气晷长之和为10.5尺，则立秋的晷长为（ ）

    A.1.5尺B.2.5尺C.3.5尺D.4.5尺

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在中，，，，分别为，的中点是由绕直线旋转得到，连结，，.

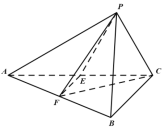
    （1）证明：平面；

    （2）若，棱上是否存在一点，使得？若存在，确定点 的位置；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x-85.71，则下列结论中不正确的是

    A. y与x具有正的线性相关关系

    B. 回归直线过样本点的中心（，）

    C. 若该大学某女生身高增加1cm，则其体重约增加0.85kg

    D. 若该大学某女生身高为170cm，则可断定其体重比为58.79kg

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在中，，，，分别为，的中点是由绕直线旋转得到，连结，，.

    （1）证明：平面；

    （2）若，棱上是否存在一点，使得？若存在，确定点 的位置；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：

    锻炼人次

    空气质量等级

    [0，200]

    (200，400]

    (400，600]

    1（优）

    2

    16

    25

    2（良）

    5

    10

    12

    3（轻度污染）

    6

    7

    8

    4（中度污染）

    7

    2

    0

    （1）分别估计该市一天的空气质量等级为1，2，3，4的概率；

    （2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；

    （3）若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？

    人次≤400

    人次>400

    空气质量好

    空气质量不好

    附：，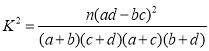

    P(K2≥k)

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    查看答案和解析>>

    同步练习册答案