
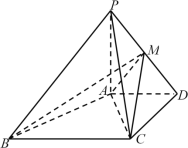
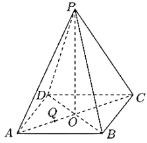
【题目】如图,在四棱锥中![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]()
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,如果存在,求
,如果存在,求![]() 与平面
与平面![]() 所成的角的正弦值,如果不存在,请说明理由.
所成的角的正弦值,如果不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]() .
.
【解析】
(1)利用直角梯形的性质求出![]() ,
,![]() 的长,根据勾股定理的逆定理得出
的长,根据勾股定理的逆定理得出![]() ,由
,由![]() 平面
平面![]() 得出
得出![]() ,故
,故![]() 平面
平面![]() ,于是
,于是![]() ;
;
(2)假设存在点![]() ,做出二面角的平面角,根据勾股定理求出
,做出二面角的平面角,根据勾股定理求出![]() 到平面
到平面![]() 的距离从而确定
的距离从而确定![]() 的位置,利用棱锥的体积求出
的位置,利用棱锥的体积求出![]() 到平面
到平面![]() 的距离
的距离![]() ,根据勾股定理计算
,根据勾股定理计算![]() ,则
,则![]() 即为所求角的正弦值.
即为所求角的正弦值.
解:(1)如图,由已知得四边形ABCD是直角梯形,
由已知![]() ,
,![]()
可得![]() 是等腰直角三角形,即
是等腰直角三角形,即![]() ,
,
又![]() 平面ABCD,则
平面ABCD,则![]() ,
,
所以![]() 平面PAC,
平面PAC,
所以![]() .
.
(2)假设存在符合条件的点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,
![]() 平面
平面![]() ,
,![]() .
.
过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 平面
平面![]() ,
,
![]() ,即
,即![]() 是二面角
是二面角![]() 的平面角.
的平面角.
若![]() ,则
,则![]() ,又
,又![]() ,
,
![]() ,即
,即![]() 是线段
是线段![]() 的中点.
的中点.
![]() 存在点
存在点![]() 使得二面角
使得二面角![]() 的大小为
的大小为![]() .
.
在三棱锥![]() 中,
中,![]() ,
,
设点![]() 到平面
到平面![]() 的距离是
的距离是![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,解得
,解得![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别是
的两个焦点分别是![]() ,直线
,直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)若![]() 为椭圆短轴上的一个顶点,且
为椭圆短轴上的一个顶点,且![]() 是直角三角形,求
是直角三角形,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】BMI指数(身体质量指数,英文为BodyMassIndex,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方.根据中国肥胖问题工作组标准,当BMI≥28时为肥胖.某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,被调查者的频率分布直方图如下:
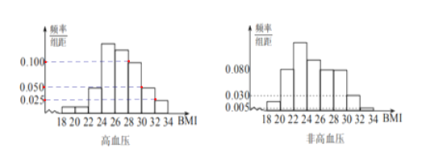
(1)求被调查者中肥胖人群的BMI平均值![]() ;
;
(2)填写下面列联表,并判断是否有99.9%的把握认为35岁以上成人患高血压与肥胖有关.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合计 | |
高血压 | |||
非高血压 | |||
合计 |
附: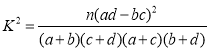 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
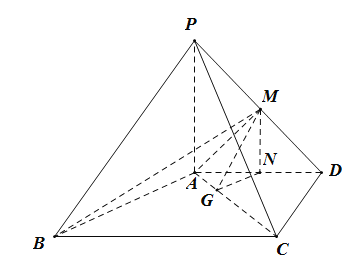
【题目】正四棱锥![]() 的底面正方形边长是3,
的底面正方形边长是3,![]() 是在底面上的射影,
是在底面上的射影,![]() ,
,![]() 是
是![]() 上的一点,过
上的一点,过![]() 且与
且与![]() 、
、![]() 都平行的截面为五边形
都平行的截面为五边形![]() .
.
(1)在图中作出截面![]() ,并写出作图过程;
,并写出作图过程;
(2)求该截面面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,以
时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)与![]() 平行的直线
平行的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,若平行线
两点,若平行线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,且
,且![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍(O为坐标原点),求
倍(O为坐标原点),求![]() 和
和![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是空气质量的一个重要指标,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35μg/m3以下空气质量为一级,在35μg/m3~75μg/m3之间空气质量为二级,在75μg/m3以上空气质量为超标.如图是某市2019年12月1日到10日PM2.5日均值(单位:μg/m3)的统计数据,则下列叙述不正确的是( )
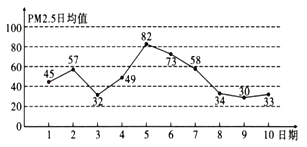
A.这10天中,12月5日的空气质量超标
B.这10天中有5天空气质量为二级
C.从5日到10日,PM2.5日均值逐渐降低
D.这10天的PM2.5日均值的中位数是47
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当![]() 数值大于或等于20.5时,我们说体重较重,当
数值大于或等于20.5时,我们说体重较重,当![]() 数值小于20.5时,我们说体重较轻,身高大于或等于
数值小于20.5时,我们说体重较轻,身高大于或等于![]() 我们说身高较高,身高小于170cm我们说身高较矮.
我们说身高较高,身高小于170cm我们说身高较矮.
(Ⅰ)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有
指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有![]() 的把握认为男生的身高对
的把握认为男生的身高对![]() 指数有影响.
指数有影响.

身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(Ⅱ)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求
.利用已经求得的线性回归方程,请完善下列残差表,并求![]() (解释变量(身高)对于预报变量(体重)变化的贡献值)(保留两位有效数字);
(解释变量(身高)对于预报变量(体重)变化的贡献值)(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重(kg) | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 |
|
|
|
|
|
|
|
②通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误,已知通过重新采集发现,该组数据的体重应该为![]() .小明重新根据最小二乘法的思想与公式,已算出
.小明重新根据最小二乘法的思想与公式,已算出![]() ,请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程.
,请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程.
参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式: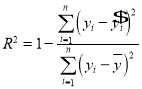 ,
,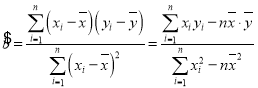 ,
,![]() ,
,![]() ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
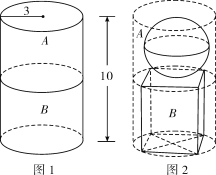
【题目】石雕工艺承载着几千年的中国石雕文化,随着科技的发展,机器雕刻产品越来越多.某石雕厂计划利用一个圆柱形的石材(如图1)雕刻制作一件工艺品(如图2),该作品的上方是一个球体,下方是一个正四棱柱,经测量,圆柱形石材的底面半径![]() 米,高
米,高![]() 米,制作要求如下:首先需将石材切割为体积相等的两部分(分别称为圆柱A和圆柱B),要求切面与原石材的上、下底面平行(不考虑损耗),然后将圆柱A切割打磨为一个球体,将圆柱B切割打磨为一个长方体,则加工打磨后所得工艺品的体积的最大值为________立方米.
米,制作要求如下:首先需将石材切割为体积相等的两部分(分别称为圆柱A和圆柱B),要求切面与原石材的上、下底面平行(不考虑损耗),然后将圆柱A切割打磨为一个球体,将圆柱B切割打磨为一个长方体,则加工打磨后所得工艺品的体积的最大值为________立方米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com