
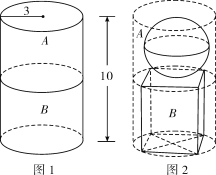
【题目】石雕工艺承载着几千年的中国石雕文化,随着科技的发展,机器雕刻产品越来越多.某石雕厂计划利用一个圆柱形的石材(如图1)雕刻制作一件工艺品(如图2),该作品的上方是一个球体,下方是一个正四棱柱,经测量,圆柱形石材的底面半径![]() 米,高
米,高![]() 米,制作要求如下:首先需将石材切割为体积相等的两部分(分别称为圆柱A和圆柱B),要求切面与原石材的上、下底面平行(不考虑损耗),然后将圆柱A切割打磨为一个球体,将圆柱B切割打磨为一个长方体,则加工打磨后所得工艺品的体积的最大值为________立方米.
米,制作要求如下:首先需将石材切割为体积相等的两部分(分别称为圆柱A和圆柱B),要求切面与原石材的上、下底面平行(不考虑损耗),然后将圆柱A切割打磨为一个球体,将圆柱B切割打磨为一个长方体,则加工打磨后所得工艺品的体积的最大值为________立方米.
【答案】![]()
【解析】
要求加工打磨后所得工艺品的体积的最大值,只需上方的球与下方的长方体的体积同时取得最大值即可.
因为圆柱A和圆柱B的体积一样大,所以它们的高![]() 一样,即
一样,即![]() 米,
米,
要使工艺品的体积最大,则上方的球与下方的长方体的体积同时取得最大值,
设由圆柱A打磨的球体半径为![]() ,则
,则![]() ,即
,即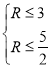 ,所以
,所以![]() ,
,
当![]() 时,球的体积取得最大值,此时球体体积
时,球的体积取得最大值,此时球体体积![]() ,
,
设下方的长方体的底面边长分别为![]() ,
,![]() ,
,
要使长方体的体积最大,长方体的高与圆柱B的高相等,此时其体积![]() ,
,
因为长方体为圆柱B的内接长方体,即长方体的底面是圆柱底面的内接长方形,
所以长方形的对角线长等于圆柱底面的直径,即![]() ,
,
由基本不等式可得![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以长方体体积的最大值为![]() ,
,
所以所得工艺品的体积的最大值为![]() (立方米).
(立方米).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]()
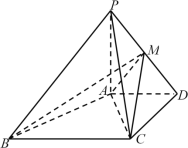
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,如果存在,求
,如果存在,求![]() 与平面
与平面![]() 所成的角的正弦值,如果不存在,请说明理由.
所成的角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点![]() 是由
是由![]() 绕直线
绕直线![]() 旋转得到,连结
旋转得到,连结![]() ,
,![]() ,
,![]() .
.
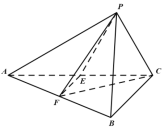
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )

A.3699块B.3474块C.3402块D.3339块
查看答案和解析>>
科目:高中数学 来源: 题型:
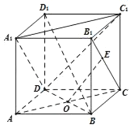
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则
①OE⊥BD1;
②OE![]() 面A1C1D;
面A1C1D;
③三棱锥A1﹣BDE的体积不是定值;
④OE与A1C1所成的最大角为90°.
上述命题中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 | [0,200] | (200,400] | (400,600] |
1(优) | 2 | 16 | 25 |
2(良) | 5 | 10 | 12 |
3(轻度污染) | 6 | 7 | 8 |
4(中度污染) | 7 | 2 | 0 |
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
人次≤400 | 人次>400 | |
空气质量好 | ||
空气质量不好 |
附: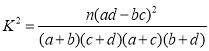 ,
,
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com