
分析 (1)利用三角形内角和公式消去A,结合正弦定理即可求解b的值.
(2)若B=$\frac{π}{3}$,利用正弦定理把a,c表示出来,转化为函数问题求解△ABC周长的范围.
解答 解:由$3cosC+ccosB=\frac{3sinA}{sinB}$
可得:$3cosC+ccosB=\frac{3sin(B+C)}{sinB}$
?3sinBcosC+c•sinBcosB=3sin(B+C)
?3sinBcosC+c•sinBcosB=3sinBcosC+3sinCcosB
?c•sinBcosB=3sinCcosB
∵$B≠\frac{π}{2}$,
∴cosB≠0,
∴c•sinB=3sinC.
正弦定理可得:bsinC=3sinC,
∴b=3
(2)由(1)得b=3,B=$\frac{π}{3}$,
∴0<A+C$<\frac{2π}{3}$
正弦定理可得:a=2$\sqrt{3}$sinA,c=2$\sqrt{3}$sinC,
那么:△ABC周长l=3+2$\sqrt{3}$(sinA+sinC)=3$+2\sqrt{3}$[sinA+sin($\frac{2π}{3}$-A)]=3$+2\sqrt{3}$[sinA+sin$\frac{2π}{3}$cosA-sinAcos$\frac{2π}{3}$)]=$3+2\sqrt{3}$[$\frac{3}{2}$sinA+$\frac{\sqrt{3}}{2}$cosA]=$3\sqrt{3}$sinA+3cosA+3=6sin(A+$\frac{π}{6}$)+3,
∵$0<A<\frac{2π}{3}$
∴$\frac{π}{6}$<A+$\frac{π}{6}$<$\frac{5π}{6}$
sin(A+$\frac{π}{6}$)∈($\frac{1}{2}$,1]
∴△ABC周长的范围是(6,9]
点评 本题考查了正弦定理和的三角形内角和定理的灵活运用,利用三角函数的有界限求解取值范围问题.属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC交于点M,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.
如图,在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC交于点M,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
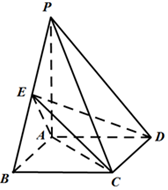 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [-1,0) | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com