
求过点(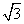 ,-
,-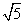 ),且与椭圆
),且与椭圆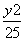 +
+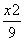 =1有相同焦点的椭圆的标准方程.
=1有相同焦点的椭圆的标准方程.
解 法一 椭圆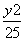 +
+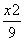 =1的焦点为(0,-4),(0,4),即c=4.由椭圆的定义知,
=1的焦点为(0,-4),(0,4),即c=4.由椭圆的定义知,
2a=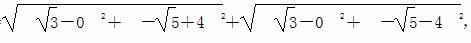
解得a=2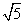 .由c2=a2-b2可得b2=4.
.由c2=a2-b2可得b2=4.
所以所求椭圆的标准方程为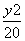 +
+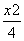 =1.
=1.
法二 因为所求椭圆与椭圆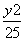 +
+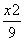 =1的焦点相同,所以其焦点在y轴上,且c2=25-9=16.
=1的焦点相同,所以其焦点在y轴上,且c2=25-9=16.
设它的标准方程为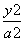 +
+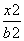 =1(a>b>0).
=1(a>b>0).
因为c2=16,且c2=a2-b2,故a2-b2=16.①
又点(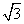 ,-
,-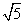 )在所求椭圆上,
)在所求椭圆上,
所以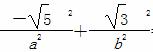 =1,即
=1,即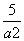 +
+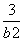 =1.②
=1.②
由①②得b2=4,a2=20,
所以所求椭圆的标准方程为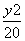 +
+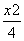 =1.
=1.
规律方法 (1)一般地,解决与到焦点的距离有关问题时,首先应考虑用定义来解决.
(2)求椭圆的标准方程有两种方法
①定义法:根据椭圆的定义,确定a2,b2的值,结合焦点位置可写出椭圆方程.
②待定系数法:若焦点位置明确,则可设出椭圆的标准方程,结合已知条件求出a,b;若焦点位置不明确,则需要分焦点在x轴上和y轴上两种情况讨论,也可设椭圆的方程为Ax2+By2=1(A>0,B>0,A≠B).


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
(1)已知直线l过点P(3,4)且与点A(-2,2),B(4,-2)等距离,则直线l的方程为( ).
A.2x+3y-18=0
B.2x-y-2=0
C.3x-2y+18=0或x+2y+2=0
D.2x+3y-18=0或2x-y-2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点F的距离为5,则以M为圆心且与y轴相切的圆的方程为( ).
A.(x-1)2+(y-4)2=1
B.(x-1)2+(y+4)2=1
C.(x-1)2+(y-4)2=16
D.(x-1)2+(y+4)2=16
查看答案和解析>>
科目:高中数学 来源: 题型:
若圆x2+y2+2x-4y+m=0(m<3)的一条弦AB的中点为P(0,1),则垂直于AB的直径所在直线的方程为( ).
A.x-y+1=0 B.x+y-1=0
C.x-y-1=0 D.x+y+1=0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点P(x0,y0),圆O:x2+y2=r2(r>0),直线l:x0x+y0y=r2,有以下几个结论:①若点P在圆O上,则直线l与圆O相切;②若点P在圆O外,则直线l与圆O相离;③若点P在圆O内,则直线l与圆O相交;④无论点P在何处,直线l与圆O恒相切,其中正确的个数是( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点.若A是PB的中点,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
一个椭圆中心在原点,焦点F1,F2在x轴上,P(2,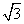 )是椭圆上一点,且|PF1|,|F1F2|,|PF2|成等差数列,则椭圆方程为( ).
)是椭圆上一点,且|PF1|,|F1F2|,|PF2|成等差数列,则椭圆方程为( ).
A.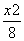 +
+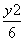 =1 B.
=1 B.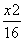 +
+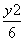 =1 C.
=1 C.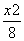 +
+ =1 D.
=1 D.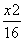 +
+ =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
根据下列条件,求双曲线的标准方程.
(1)虚轴长为12,离心率为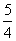 ;
;
(2)焦距为26,且经过点M(0,12).
(3)经过两点P(-3,2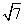 )和Q(-6
)和Q(-6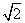 ,-7).
,-7).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com