
分析 由分段函数得f(ln$\frac{1}{4}$)=f(1+ln$\frac{1}{4}$)=f(2+ln$\frac{1}{4}$)=${e}^{(2+ln\frac{1}{4})}$,由此能求出结果.
解答 解:∵函数f(x)=$\left\{{\begin{array}{l}{{e^x},x>0}\\{f(x+1),x≤0}\end{array}}$,
∴f(ln$\frac{1}{4}$)=f(1+ln$\frac{1}{4}$)=f(2+ln$\frac{1}{4}$)
=${e}^{(2+ln\frac{1}{4})}$=${e}^{2}×{e}^{ln\frac{1}{4}}$=$\frac{e^2}{4}$.
故答案为:$\frac{{e}^{2}}{4}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
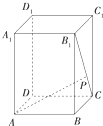 如图所示,在长方体ABCD-A1B1C1D1中,AB=2,AD=3,AA1=2$\sqrt{6}$,点P是B1C的三等分点且靠近点C,则异面直线AP和DD1所成的角为( )
如图所示,在长方体ABCD-A1B1C1D1中,AB=2,AD=3,AA1=2$\sqrt{6}$,点P是B1C的三等分点且靠近点C,则异面直线AP和DD1所成的角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
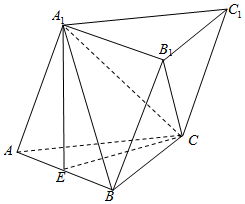 在斜三棱柱ABC-A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.
在斜三棱柱ABC-A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,3,5} | B. | {1,2,3} | C. | {0,1} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
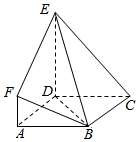 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,且DE=6,AF=2.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,且DE=6,AF=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{5}$i | B. | $\frac{2}{5}i$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
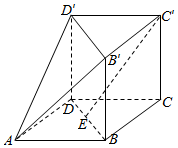 如图,所有棱长都为2的正三棱柱BCD-B'C'D',四边形ABCD是菱形,其中E为BD的中点.
如图,所有棱长都为2的正三棱柱BCD-B'C'D',四边形ABCD是菱形,其中E为BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3+2\sqrt{2}}}{4}$ | C. | $\frac{{3+\sqrt{2}}}{4}$ | D. | $\frac{{3-\sqrt{2}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com