
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3+2\sqrt{2}}}{4}$ | C. | $\frac{{3+\sqrt{2}}}{4}$ | D. | $\frac{{3-\sqrt{2}}}{4}$ |
分析 由题意可得,x与y的关系,化简所求的表达式,展开利用基本不等式即可求解.
解答 解:A、B、P是直线l上三个点,且正实数x,y满足$4\overrightarrow{OP}=2x\overrightarrow{OA}+y\overrightarrow{OB}$,
可得:$\frac{x}{2}+\frac{y}{4}=1$,
则$\frac{1}{x}+\frac{1}{y}$=($\frac{1}{x}+\frac{1}{y}$)($\frac{x}{2}+\frac{y}{4}$)=$\frac{1}{2}+\frac{1}{4}$+$\frac{x}{2y}$+$\frac{y}{4x}$
≥$\frac{1}{2}+\frac{1}{4}$+2$\sqrt{\frac{x}{2y}•\frac{y}{4x}}$=$\frac{3}{4}$$+\frac{\sqrt{2}}{2}$=$\frac{3+2\sqrt{2}}{4}$,
当且仅当$\frac{x}{2y}=\frac{y}{4x}$,即y=$\sqrt{2}$x,
此时x=4-2$\sqrt{2}$,y=4$\sqrt{2}$-4时取等号.
故选:B.
点评 本题主要考查了向量的共线定理的应用,基本不等式求解最值的应用,解题的关键是$\frac{1}{2}$x+$\frac{1}{4}$y=1.


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
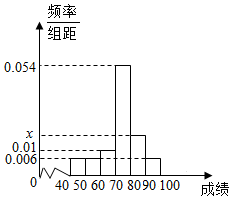 如图是某班50位学生期中考试化学成绩的频率分布直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[70,90)内的频数为( )
如图是某班50位学生期中考试化学成绩的频率分布直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[70,90)内的频数为( )| A. | 27 | B. | 30 | C. | 32 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
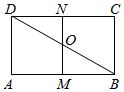 如图,矩形ABCD中AB=2,BC=$\frac{{2\sqrt{3}}}{3}$,M,N分别为AB,CD中点,BD与MN交于O,现将矩形沿MN折起,使得二面角A-MN-B的大小为$\frac{π}{3}$,则折起后cos∠DOB为( )
如图,矩形ABCD中AB=2,BC=$\frac{{2\sqrt{3}}}{3}$,M,N分别为AB,CD中点,BD与MN交于O,现将矩形沿MN折起,使得二面角A-MN-B的大小为$\frac{π}{3}$,则折起后cos∠DOB为( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
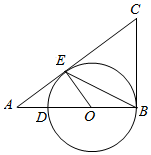 如图,E为⊙O上一点,点A在直径BD的延长线上,过点B作⊙O的切线交AE的延长线于点C,CE=CB.
如图,E为⊙O上一点,点A在直径BD的延长线上,过点B作⊙O的切线交AE的延长线于点C,CE=CB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com