
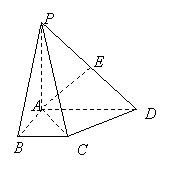
如图,在四棱锥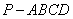 中,
中,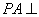 平面
平面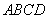 ,底面
,底面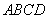 是直角梯形,
是直角梯形,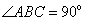 ,
, ∥
∥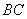 ,且
,且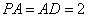 ,
,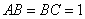 ,
, 为
为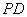 的中点.
的中点.
(Ⅰ)设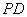 与平面
与平面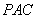 所成的角为
所成的角为 ,二面角
,二面角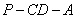 的
的
大小为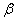 ,求证:
,求证: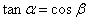 ;
;
(Ⅱ)在线段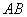 上是否存在一点
上是否存在一点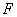 (与
(与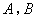 两点不重合),使得
两点不重合),使得
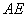 ∥平面
∥平面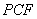 ? 若存在,求
? 若存在,求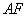 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
为了了解某校九年级1600名学生的体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
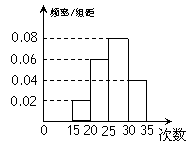

A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数 在(0,+
在(0,+ )内有定义,对于给定的正数K,定义函数
)内有定义,对于给定的正数K,定义函数 ,取函数
,取函数 ,恒有
,恒有 ,则
,则
A.K的最大值为 B.K的最小值为
B.K的最小值为
C.K的最大值为2 D.K的最小值为2
查看答案和解析>>
科目:高中数学 来源: 题型:
将长度为 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时 的最大值为4.则:
的最大值为4.则:
(1)当 时,
时, 的最大值为________;(2)当
的最大值为________;(2)当 时,
时, 的最大值为________.
的最大值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)= +cos2x-sin2x.
+cos2x-sin2x.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)在所给坐标系中画出函数在区间[ π,
π, π]的图像(只作图不写过程).
π]的图像(只作图不写过程).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com