
【题目】某地4个蔬菜大棚顶部,阳光照在一棵棵茁壮生长的蔬菜上.这些采用水培、无土栽培方式种植的各类蔬菜,成为该地区居民争相购买的对象.过去50周的资料显示,该地周光照量![]() (小时)都在30以上.其中不足50的周数大约有5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周.根据统计某种改良黄瓜每个蔬菜大棚增加量
(小时)都在30以上.其中不足50的周数大约有5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周.根据统计某种改良黄瓜每个蔬菜大棚增加量![]() (百斤)与每个蔬菜大棚使用农夫1号液体肥料
(百斤)与每个蔬菜大棚使用农夫1号液体肥料![]() (千克)之间对应数据为如图所示的折线图:
(千克)之间对应数据为如图所示的折线图:
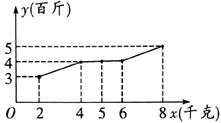
(Ⅰ)依据数据的折线图,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量
;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量![]() 是多少斤?
是多少斤?
(Ⅱ)因蔬菜大棚对光照要求较大,某光照控制仪商家为应对恶劣天气对光照的影响,为该基地提供了部分光照控制仪,该商家希望安装的光照控制仪尽可能运行,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为5000元;若某台光照控制仪未运行,则该台光照控制仪周亏损800元,欲使商家周总利润的均值达到最大,应安装光照控制仪多少台?
附:回归方程系数公式: 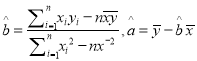 .
.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)算出样本中心点的坐标,利用公式求得![]() ,由
,由![]() 可得
可得![]() ,即可得回归方程,再将
,即可得回归方程,再将![]() 时代入即可得结果;(Ⅱ)分别求出安装2台光照控制仪的周利润的均值、安装3台光照控制仪的均值,与安装1台光照控制仪可获得周利润进行比较即可得结果.
时代入即可得结果;(Ⅱ)分别求出安装2台光照控制仪的周利润的均值、安装3台光照控制仪的均值,与安装1台光照控制仪可获得周利润进行比较即可得结果.
试题解析:(Ⅰ) ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,
,
当![]() 时,
时, ![]() 百斤=550斤,
百斤=550斤,
所以估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量![]() 是500斤.
是500斤.
(Ⅱ)记商家总利润为![]() 元,由已知条件可知至少需安装1台,
元,由已知条件可知至少需安装1台,
①安装1台光照控制仪可获得周利润5000元,
②安装2台光照控制仪的情形:
当![]() 时,一台光照控制仪运行,此时
时,一台光照控制仪运行,此时![]() 元,
元,
当![]() 时,两台光照控制仪都运行,此时
时,两台光照控制仪都运行,此时![]() 元,
元,
故![]() 的分布列为
的分布列为
| 4200 | 10000 |
| 0.2 | 0.8 |
所以![]() 元,
元,
③安装3台光照控制仪的情形:
当![]() 时,一台光照控制仪运行,此时
时,一台光照控制仪运行,此时![]() 元,
元,
当![]() 时,两台光照控制仪运行,此时
时,两台光照控制仪运行,此时![]() 元,
元,
当![]() 时,三台光照控制仪都运行,此时
时,三台光照控制仪都运行,此时![]() 元,
元,
故![]() 的分布列为
的分布列为
| 3400 | 9200 | 15000 |
| 0.2 | 0.7 | 0.1 |
所以![]() 元,
元,
综上,为使商家周总利润的均值达到最大应该安装2台光照控制仪.
【方法点晴】本题主要考查线性回归方程及离散型随机变量的分布列与数学期望,属于难题.求回归直线方程的步骤:①依据样本数据确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2x+a
(1)当 ![]() 时,求不等式f(x)>1的解集;
时,求不等式f(x)>1的解集;
(2)若对于任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲种混合肥料1车皮、乙种混合肥料1车皮所需要的主要原料如表:
原料 | 磷酸盐(单位:吨) | 硝酸盐(单位:吨) |
甲 | 4 | 20 |
乙 | 2 | 20 |
现库存磷酸盐8吨、硝酸盐60吨,计划在此基础上生产若干车皮的甲、乙两种混合肥料.
(1)设x,y分别表示计划生产甲、乙两种肥料的车皮数,试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)若生产1车皮甲种肥料,利润为3万元;生产1车皮乙种肥料,利润为2万元.那么分别生产甲、乙两种肥料多少车皮,能够产生最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=3ax2﹣2(a+b)x+b,(0≤x≤1)其中a>0,b为任意常数.
(I)若b= ![]() ,f(x)=|x﹣
,f(x)=|x﹣ ![]() |在x∈[0,1]有两个不同的解,求实数a的范围.
|在x∈[0,1]有两个不同的解,求实数a的范围.
(II)当|f(0)|≤2,|f(1)|≤2时,求|f(x)|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行抽奖活动,从装有编号0,1,2,3四个小球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com