
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}e$ | C. | e | D. | 2e |
分析 通过参数分离,利用基本不等式放缩可知问题转化为2lna≤$\frac{3+{e}^{x-4}}{x}$在x>0时恒成立,记g(x)=$\frac{3+{e}^{x-4}}{x}$,二次求导并结合单调性可知当x=4时g(x)取得最小值g(4)=1,进而计算即得结论.
解答 解:设f(x)=ex+y-4+ex-y-4+6,则问题转化为不等式4xlna≤f(x)恒成立.
又∵f(x)=ex-4(ey+e-y)+6≥6+2ex-4(当且仅当y=0时取等号),
∴4xlna≤6+2ex-4,即有2lna≤$\frac{3+{e}^{x-4}}{x}$在x>0时恒成立,
记g(x)=$\frac{3+{e}^{x-4}}{x}$,则g′(x)=$\frac{{e}^{x-4}(x-1)-3}{{x}^{2}}$,
令g′(x)=0,即(x-1)ex-4=3,
记h(x)=(x-1)ex-4,则h′(x)=xex-4,
∵x>0,ex-4>0,
∴h′(x)>0,∴h(x)在(0,+∞)上单调递增,
又∵h(4)=3,即有(x-1)ex-4=3的根为4,
∴当x>4时g(x)递增,当0<x<4时g(x)递减,
∴当x=4时,g(x)取得最小值g(4)=1,
∴2lna≤1,lna≤$\frac{1}{2}$,
∴0<a≤$\sqrt{e}$,(当x=2,y=0时,a取得最大值$\sqrt{e}$),
故选:A.
点评 本题考查不等式恒成立问题的常用方法是注意转化为求函数的最值问题,运用参数分离和构造函数再利用导数判断单调性是解题的关键,注意解题方法的积累,属于难题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{13}}}{2}$ | B. | $\frac{3}{2}$ | C. | $1+\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
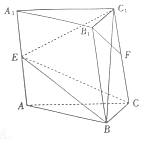 如图,已知直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1,CC1的中点,且BE⊥B1F.
如图,已知直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1,CC1的中点,且BE⊥B1F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
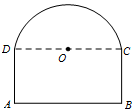 某隧道截面如图,其下部形状是矩形ABCD,上部形状是以CD为直径的半圆.已知隧道的横截面面积为4+π,设半圆的半径OC=x,隧道横截面的周长(即矩形三边长与圆弧长之和)为f(x).
某隧道截面如图,其下部形状是矩形ABCD,上部形状是以CD为直径的半圆.已知隧道的横截面面积为4+π,设半圆的半径OC=x,隧道横截面的周长(即矩形三边长与圆弧长之和)为f(x).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,4) | B. | (4,6] | C. | (-4,6) | D. | (-4,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com