
分析 通过目标函数z=x2+y2即表示以原点O为圆心与满足约束条件的变量x、y所构成的梯形ABCD相交的圆的半径的平方,进而计算即得结论.
解答 解:依题意,满足约束条件的变量x、y所构成的图形为梯形ABCD,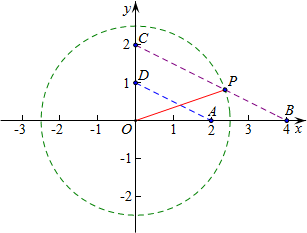
其中A(2,0),B(4,0),C(0,2),D(0,1),
则目标函数z=x2+y2即表示以原点O为圆心与梯形ABCD相交的圆的半径的平方,
∴z的最小值为原点O到直线AD的距离d的平方,
最大值为OB2=16,
∵$\frac{1}{2}•d•AD=\frac{1}{2}OA•OD$,
∴d=$\frac{2×1}{\sqrt{{1}^{2}+{2}^{2}}}$=$\frac{2}{\sqrt{5}}$,即d2=$\frac{4}{5}$,
∴$\frac{4}{5}$<z<16,
故答案为:($\frac{4}{5}$,16).
点评 本题考查简单线性规划,考查数形结合能力,注意解题方法的积累,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
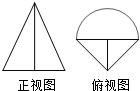 由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )
由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )| A. | $\frac{π}{2}+1$ | B. | π+1 | C. | $\frac{π}{2}+3$ | D. | π+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 8-$\frac{2π}{3}$ | B. | 8-$\frac{π}{3}$ | C. | 8-2π | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 72一$\frac{9π}{2}$ | B. | 72-4π | C. | 72一$\frac{7π}{2}$ | D. | 72-3π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{9}{4}$) | B. | (-∞,-$\frac{9}{4}$] | C. | [-$\frac{9}{4}$,+∞) | D. | [0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com