
| 3 |
| 2 |
| 5 |
| 2 |
| π |
| 8 |
| 5π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| 3 |
| 2 |
| 5π |
| 2 |
| π |
| 2 |
| 5π |
| 4 |
| 5π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| kπ |
| 2 |
| π |
| 8 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 5 |
| AM |
| AB |
| AN |
| AC |
| 1 |
| x |
| 1 |
| y |
| ∫ | π 0 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:全优设计必修四数学苏教版 苏教版 题型:013
给出下列六个命题,其中不正确的命题的个数为
①两个向量相等,则它们的起点相同,终点相同;
②若|a|=|b|,则a=b;
③若![]() =
=![]() ,则四边形ABCD是平行四边形;
,则四边形ABCD是平行四边形;
④平行四边形ABCD中,一定有![]() =
=![]() ;
;
⑤若m=n,n=k,则m=k;
⑥若a∥b,b∥c,则a∥c.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 3 |
| 2 |
| 5 |
| 2 |
| π |
| 8 |
| 5π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:《第1章 三角函数-第3章 三角恒等变换》2010年单元测试卷(解析版) 题型:填空题
 ;
; π-2x)是偶函数;
π-2x)是偶函数;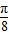 是y=sin(2x+
是y=sin(2x+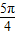 )的一条对称轴;
)的一条对称轴;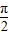 )上的增函数;
)上的增函数;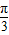 )的图象可由y=3sin2x的图象向左平移
)的图象可由y=3sin2x的图象向左平移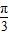 个单位得到.
个单位得到.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com