
【题目】设函数![]() 的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
(1)求(RA)∩B;
(2)若(A∪B)∩C≠,求实数m的取值范围.
【答案】(1){x|x≤2或x>3}(2)m≤3
【解析】
试题分析:(1)首先求定义域得到集合A,A的补集为全集中除去A中元素剩余的元素构成的集合,两集合的交集为两集合相同的元素构成的集合;(2)首先求得A∪B,由(A∪B)∩C≠可知A∪B与C有相同的元素,由此可得到m的不等式,求得其取值范围
试题解析:(1)因0<a<1,由loga(x﹣2)≥0得0<x﹣2≤1,
所以A={x|2<x≤3},…………………………………3分
CRA={x|x≤2或x>3},…………………………………5分
(CRA)∩B={x|x≤2或x>3}∩{x|1<x<3}={x|1<x≤2},……………7分
(2)由(1)知A={x|2<x≤3},因B={x|1<x<3},
所以A∪B={x|1<x≤3},…………………9分
又C={x|x≥m},(A∪B)∩C≠,
所以m≤3,…………………………………12分


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】“x2-3x+2<0”是“-1<x<2”成立的______条件(在“充分不必要”,“必要不充分”,“充要”,“既不充分又不必要”中选一个填写).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xln x.
(1)求函数f(x)的极值点;
(2)设函数g(x)=f(x)-a(x-1),其中a∈R,求函数g(x)在区间[1,e]上的最小值.(其中e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有3个黑球,4个白球,从中任取4个球,则
①至少有1个白球和至少有1个黑球; ②至少有2个白球和恰有3个黑球;
③至少有1个黑球和全是白球; ④恰有1个白球和至多有1个黑球.
在上述事件中,是互斥事件但不是对立事件的为( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有6个红球和5个白球的口袋中任取4个球,那么下列是互斥而不对立的事件是( )
A. 至少一个红球与都是红球
B. 至少一个红球与至少一个白球
C. 至少一个红球与都是白球
D. 恰有一个红球与恰有两个红球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() .
.
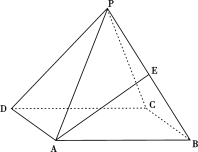
(1)求正四棱锥![]() 的外接球半径;
的外接球半径;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某篮球比赛中,根据甲和乙两人的得分情况得到如图所示的茎叶图.

(1)从茎叶图的特征来说明他们谁发挥得更稳定;
(2)用样本的数字特征验证他们谁发挥得更好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com