
已知函数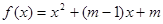 ,
,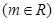
(1)若 是偶函数,求
是偶函数,求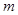 的值。
的值。
(2)设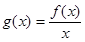 ,
,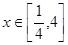 ,求
,求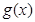 的最小值。
的最小值。
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知函数 处取得极值2。
处取得极值2。
(Ⅰ) 求函数
求函数 的表达式;
的表达式;
(Ⅱ)当 满足什么条件时,函数
满足什么条件时,函数 在区间
在区间 上单调递增?
上单调递增?
(Ⅲ)若 为
为 图象上任意一点,直线与
图象上任意一点,直线与 的图象切于点P,求直线的斜率
的图象切于点P,求直线的斜率 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本题12分)
已知函数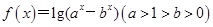 .
.
(1)求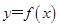 的定义域;
的定义域;
(2)在函数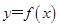 的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当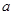 ,b满足什么条件时,
,b满足什么条件时,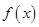 在
在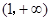 上恒取正值.
上恒取正值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在(-∞,—1)∪(1,+∞)上的奇函数满足:①f(3)=1;②对任意的x>2, 均有f(x)>0,③对任意的x>0,y>0.均有f(x+1)+f(y+1)=f(xy+1)
⑴试求f(2)的值;
⑵证明f(x)在(1,+∞)上单调递增;
⑶是否存在实数a,使得f(cos2θ+asinθ)<3对任意的θ (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某工厂用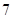 万元钱购买了一台新机器,运输安装费用
万元钱购买了一台新机器,运输安装费用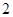 千元,每年投保、动力消耗的费用也为
千元,每年投保、动力消耗的费用也为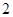 千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为
千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为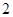 千元,第二年为
千元,第二年为 千元,第三年为
千元,第三年为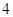 千元,依此类推,即每年增加
千元,依此类推,即每年增加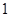 千元.
千元.
(Ⅰ)求使用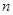 年后,保养、维修、更换易损零件的累计费用S(千元)关于
年后,保养、维修、更换易损零件的累计费用S(千元)关于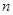 的表达式;
的表达式;
(Ⅱ)问这台机器最佳使用年限是多少年?并求出年平均费用(单位:千元)的最小值.(最佳使用年限是指使年平均费用最小的时间,年平均费用=(购入机器费用+运输安装费用+每年投保、动力消耗的费用+保养、维修、更换易损零件的累计费用)÷机器使用的年数 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com