
(本小题满分12分)某工厂用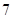 万元钱购买了一台新机器,运输安装费用
万元钱购买了一台新机器,运输安装费用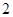 千元,每年投保、动力消耗的费用也为
千元,每年投保、动力消耗的费用也为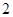 千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为
千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为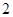 千元,第二年为
千元,第二年为 千元,第三年为
千元,第三年为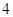 千元,依此类推,即每年增加
千元,依此类推,即每年增加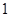 千元.
千元.
(Ⅰ)求使用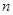 年后,保养、维修、更换易损零件的累计费用S(千元)关于
年后,保养、维修、更换易损零件的累计费用S(千元)关于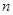 的表达式;
的表达式;
(Ⅱ)问这台机器最佳使用年限是多少年?并求出年平均费用(单位:千元)的最小值.(最佳使用年限是指使年平均费用最小的时间,年平均费用=(购入机器费用+运输安装费用+每年投保、动力消耗的费用+保养、维修、更换易损零件的累计费用)÷机器使用的年数 )
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)如下左图,已知底角为450的等腰三角形ABC,底边AB的长为2,当一条垂直于AB的直线L从左至右移动时,直线L把三角形ABC分成两部分,令AD=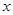 ,
,
(1) 试写出左边部分的面积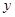 与x的函数解析式;
与x的函数解析式;
(2) 在给出的坐标系中画出函数的大致图象。 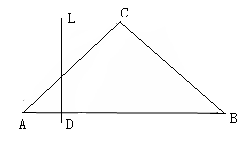
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)用分段函数的形式表示该函数;
(2)在右边所给的坐标系中画出该函数的图象;
(3)写出该函数的定义域、值域、奇偶性、单调区间(不要求证明). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com