
(本小题满分12分)已知函数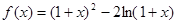 .
.
(1)若定义域内存在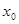 ,使不等式
,使不等式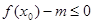 成立,求实数
成立,求实数 的最小值;
的最小值;
(2)若函数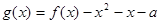 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 取值范围.
取值范围.
(1) (2)
(2)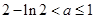
解析试题分析:(1)因为定义域内存在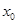 ,使不等式
,使不等式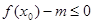 成立,所以
成立,所以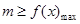 .
.
由已知得,函数 的定义域为
的定义域为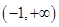 ,
,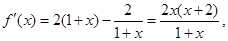
令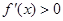 得
得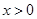 ,令
,令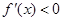 得
得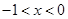 ,
,
∴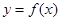 在
在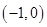 上单调递减,在
上单调递减,在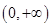 上单调递增,
上单调递增,
所以 ,所以
,所以 ,即实数
,即实数 的最小值为
的最小值为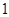 . ---5分
. ---5分
(2)因为函数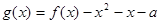 在区间
在区间 上恰有两个不同的零点,
上恰有两个不同的零点,
所以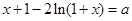 有两个不相等的实数根.
有两个不相等的实数根.
令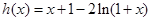 ,所以
,所以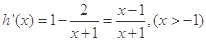 ,
,
所以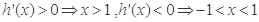
∴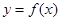 在[0,1]上单调递减,在(1,3]上单调递增,
在[0,1]上单调递减,在(1,3]上单调递增,
而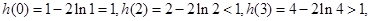
∴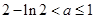 . ---12分
. ---12分
考点:本小题主要考查不等式恒成立问题和函数的零点问题以及利用导数考查函数的单调性及最值问题,考查学生综合运用知识分析问题解决问题的能力和转化问题的能力.
点评:不等式的恒成立问题往往转化为最值问题来解决,而函数零点问题往往转化为两函数图象的交点个数问题.
请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑.


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
(1)已知函数f(x)=2x-x2,问方程f(x)=0在区间[-1,0]内是否有解,为什么?
(2)若方程ax2-x-1=0在(0,1)内恰有一解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设函数f (x)=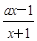 ,其中a∈R.
,其中a∈R.
(1)若a=1,f (x)的定义域为[0,3],求f (x)的最大值和最小值.
(2)若函数f (x)的定义域为区间(0,+∞),求a的取值范围使f (x)在定义域内是单调减函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com