
(本小题满分12分)
(1)已知函数f(x)=2x-x2,问方程f(x)=0在区间[-1,0]内是否有解,为什么?
(2)若方程ax2-x-1=0在(0,1)内恰有一解,求实数a的取值范围.
(1) 方程f(x)=0在区间[-1,0]内有解.(2) (2,+∞).
解析试题分析:
(1)因为第一问中,f(-1)=2-1-(-1)2=-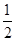 <0,
<0,
f(0)=20-02=1>0,结合零点存在性定理可知,结论。
(2)方程ax2-x-1=0在(0,1)内恰有一解,即函数f(x)=ax2-x-1在(0,1)内恰有一个零点,则只要满足端点的函数值一号即可。
(1) 因为f(-1)=2-1-(-1)2=-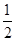 <0,
<0,
f(0)=20-02=1>0,
而函数f(x)=2x-x2的图象是连续曲线,所以f(x)在区间[-1,0]内有零点,即方程f(x)=0在区间[-1,0]内有解.
(2)∵方程ax2-x-1=0在(0,1)内恰有一解,即函数f(x)=ax2-x-1在(0,1)内恰有一个零点,
∴f(0)·f(1)<0,即-1×(a-2)<0,解得a>2.
故a的取值范围为(2,+∞).
考点:本题主要是考查函数零点的运用。
点评:解决该试题的关键是根据零点的概念将方程解的问题转换为关于图像与图像的交点问题来处理得到结论。


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分)已知函数 的一系列对应值如下表:
的一系列对应值如下表:
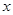 |  |  |  |  |  |  |  |
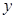 |  |  |  |  |  |  |  |
 的解析式;
的解析式; 周期为
周期为 ,求
,求 在区间
在区间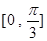 上的最大、最小值及对应的
上的最大、最小值及对应的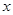 的值.
的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本题12分)
已知函数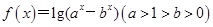 .
.
(1)求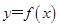 的定义域;
的定义域;
(2)在函数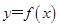 的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当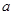 ,b满足什么条件时,
,b满足什么条件时,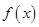 在
在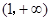 上恒取正值.
上恒取正值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在(-∞,—1)∪(1,+∞)上的奇函数满足:①f(3)=1;②对任意的x>2, 均有f(x)>0,③对任意的x>0,y>0.均有f(x+1)+f(y+1)=f(xy+1)
⑴试求f(2)的值;
⑵证明f(x)在(1,+∞)上单调递增;
⑶是否存在实数a,使得f(cos2θ+asinθ)<3对任意的θ (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com