
(本小题满分13分)
已知函数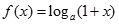 ,
,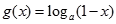 ,
,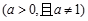 .
.
(Ⅰ)设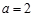 ,函数
,函数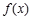 的定义域为
的定义域为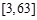 ,求函数
,求函数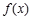 的最值;
的最值;
(Ⅱ)求使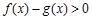 的
的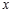 的取值范围.
的取值范围.
(I)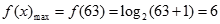 ,
,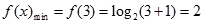
(II)①当 时,
时, 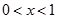 ;②当
;②当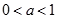 时,
时, 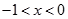 。
。
解析试题分析:(1)根据对数函数定义域,和单调性得到函数的最值(2)对于底数a,由于不定,需要分情况来讨论得到。
解
(I)当 时,函数
时,函数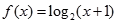 为
为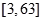 上的增函数........................3分
上的增函数........................3分
故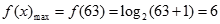 ,
,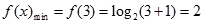 ..........................................6分
..........................................6分
(II) ,即
,即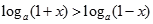 ,
,
①当 时,
时, ,得
,得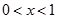 ........................................9分
........................................9分
②当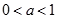 时,
时, ,得
,得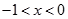 ..........................13分
..........................13分
考点:本试题主要考查了对数函数定义域的求解以及对数不等式的求解。
点评:解决该试题的关键是利用底数的大于1,还是底数大于零小于1,分情况来解决对数不等式的求解。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
(1)已知函数f(x)=2x-x2,问方程f(x)=0在区间[-1,0]内是否有解,为什么?
(2)若方程ax2-x-1=0在(0,1)内恰有一解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如下左图,已知底角为450的等腰三角形ABC,底边AB的长为2,当一条垂直于AB的直线L从左至右移动时,直线L把三角形ABC分成两部分,令AD=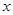 ,
,
(1) 试写出左边部分的面积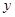 与x的函数解析式;
与x的函数解析式;
(2) 在给出的坐标系中画出函数的大致图象。 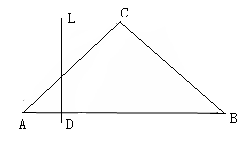
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com