已知圆C:x2+y2-4x+6y+4=0.
(1)将圆C的方程化为标准方程并指出圆心C的坐标以及半径的大小;
(2)过点P(-1,1)引圆C的切线,切点为A,求切线长|PA|;
(3)求过点P(-1,1)的圆C的切线方程.
【答案】
分析:(1)利用配方法把圆C方程的左边变形后,将圆C的方程化为标准方程,从标准方程中即可得到圆心C的坐标和圆的半径;
(2)由P和C的坐标,利用两点间的距离公式求出|PC|的长,得到|PC|小于半径r,即P在圆外,根据切线的性质及勾股定理,由|PC|及r的值,即可求出切线长|PA|的长;
(3)分两种情况考虑:当满足题意的切线方程的斜率不存在时,显然x=-1满足题意;当斜率存在时,设切线方程的斜率为k,由P的坐标和k表示出切线的方程,根据圆心到切线的距离等于圆的半径,利用点到直线的距离公式列出关于k的方程,求出方程的解即可得到k的值,确定出此时切线的方程,综上,得到所有满足题意的切线方程.
解答:解:(1)将圆C化为标准方程得:(x-2)
2+(y+3)
2=9,
∴圆心C(2,-3),半径r=3;
(2)∵|PC|=

=5>3=r,
∴P在圆C外,
则|PA|=
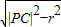
=4;
(3)当过P的圆C的切线方程的斜率不存在时,显然x=-1满足题意;
当斜率存在时,设切线的斜率为k,
∴切线方程为y-1=k(x+1),即kx-y+k+1=0,
∴圆心C到切线的距离d=r,即

=3,
解得:k=-

,
此时切线方程为:-
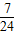
x-y-

=0,即7x+24y-17=0,
综上,满足题意的切线方程为x=-1或7x+24y-17=0、
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,两点间的距离公式,点到直线的距离公式,切线的性质,勾股定理,以及直线的点斜式方程,利用了分类讨论的思想,是一道综合性较强的题.

 =5>3=r,
=5>3=r,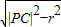 =4;
=4; =3,
=3, ,
,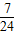 x-y-
x-y- =0,即7x+24y-17=0,
=0,即7x+24y-17=0,

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.