
【题目】已知椭圆C: ![]() =1(a>b>0)经过点(
=1(a>b>0)经过点( ![]() ,1),且离心率为
,1),且离心率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设M、N是椭圆C上的点,直线OM与ON(O为坐标原点)的斜率之积为﹣ ![]() ,若动点P满足
,若动点P满足 ![]() ,试探究,是否存在两个定点F1 , F2 , 使得|PF1|+|PF2|为定值?若存在,求F1 , F2的坐标,若不存在,请说明理由.
,试探究,是否存在两个定点F1 , F2 , 使得|PF1|+|PF2|为定值?若存在,求F1 , F2的坐标,若不存在,请说明理由.
【答案】解:(Ⅰ)∵椭圆C: ![]() =1(a>b>0)经过点(
=1(a>b>0)经过点( ![]() ,1),且离心率为
,1),且离心率为 ![]() ,
,
∴ 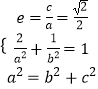 ,解得a=2,b=
,解得a=2,b= ![]() ,
,
∴椭圆C的方程为 ![]() .
.
(Ⅱ)设P(x,y),M(x1 , y1),N(x2 , y2),
则由 ![]() ,得x=x1+2x2 , y=y1+2y2 ,
,得x=x1+2x2 , y=y1+2y2 ,
∵M,N都在椭圆 ![]() 上,
上,
∴ ![]() ,
,
∴ ![]() (
( ![]() )
)
=( ![]() )+4(
)+4( ![]() )+4(x1x2+2y1y2)
)+4(x1x2+2y1y2)
=20+4(x1x2+2y1y2),
设 ![]() =﹣
=﹣ ![]() ,∴x1x2+2y1y2=0,
,∴x1x2+2y1y2=0,
∴x2+2y2=20,∴点P是椭圆 ![]() 上的点,
上的点,
∴由椭圆的定义知存在点F1 , F2 , 满足|PF1|+|PF2|=2 ![]() =4
=4 ![]() 为定值,
为定值,
又∵|F1F2|=2 ![]() =2
=2 ![]() ,
,
∴F1 , F2的坐标分别为F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0)
,0)
【解析】(Ⅰ)由椭圆经过点( ![]() ,1),且离心率为
,1),且离心率为 ![]() ,列出方程组,求出a,b,由此能求出椭圆C的方程.(Ⅱ)由
,列出方程组,求出a,b,由此能求出椭圆C的方程.(Ⅱ)由 ![]() ,得x=x1+2x2 , y=y1+2y2 , 由M,N都在椭圆
,得x=x1+2x2 , y=y1+2y2 , 由M,N都在椭圆 ![]() 上,设
上,设 ![]() =﹣
=﹣ ![]() ,得到点P是椭圆
,得到点P是椭圆 ![]() 上的点,由此能求出F1 , F2的坐标.
上的点,由此能求出F1 , F2的坐标.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1、A1B1上,且AE= ![]() ,A1F=
,A1F= ![]() ,CE⊥EF. (Ⅰ)证明:平面ABB1A1⊥平面ABC;
,CE⊥EF. (Ⅰ)证明:平面ABB1A1⊥平面ABC;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0<h<2)的平面截该几何体,则截面面积为( ) 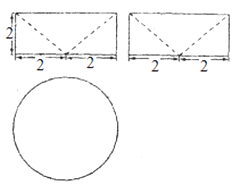
A.4π
B.πh2
C.π(2﹣h)2
D.π(4﹣h)2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣x+2 ![]() .
.
(Ⅰ)求函数y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)令g(x)= ![]() +lnx,若函数y=g(x)在(e,+∞)内有极值,求实数a的取值范围;
+lnx,若函数y=g(x)在(e,+∞)内有极值,求实数a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,对任意t∈(1,+∞),s∈(0,1),求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2为双曲线C: ![]() (a>0,b>0)的左、右焦点,点P为双曲线C右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则双曲线C的离心率为( )
(a>0,b>0)的左、右焦点,点P为双曲线C右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则双曲线C的离心率为( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的实义域为R,其图象关于点(﹣1,0)中心对称,其导函数为f′(x),当x<﹣1时,(x+1)[f(x)+(x+1)f′(x)]<0.则不等式xf(x﹣1)>f(0)的解集为( )
A.(1,+∞)
B.(﹣∞,﹣1)
C.(﹣1,1)
D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点M的直角坐标为(1,0),若直线l的极坐标方程为 ![]() ρcos(θ+
ρcos(θ+ ![]() )﹣1=0,曲线C的参数方程是
)﹣1=0,曲线C的参数方程是 ![]() (t为参数).
(t为参数).
(1)求直线l和曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中,底面ABCD是正方形,AA1=2,AB=1,E是DD1上的一点. 
(1)求异面直线AC与B1D所成的角;
(2)若B1D⊥平面ACE,求三棱锥A﹣CDE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com