
°ĺŐ‚ńŅ°Ņ◊ś≥Ś÷ģ÷ģ◊”◊śēú «ő“ĻķńŌĪĪ≥Į ĪīķőįīůĶńŅ∆—ßľ“£¨ňŻ‘ŕ ĶľýĶńĽýī°…ŌŐŠ≥ŲŃňŐŚĽżľ∆ň„Ķń‘≠ņŪ£ļ°į√› ∆ľ»Õ¨£¨‘ÚĽż≤Ľ»›“ž°Ī£ģ“‚ňľ «£¨»ÁĻŻŃĹłŲĶ»łŖĶńľłļőŐŚ‘ŕÕ¨łŖī¶ĹōĶ√ĶńĹō√ś√śĽżļ„Ķ»£¨ń«√ī’‚ŃĹłŲľłļőŐŚĶńŐŚĽżŌŗĶ»£ģīňľī◊śēú‘≠ņŪ£ģņŻ”√’‚łŲ‘≠ņŪ«ů«ÚĶńŐŚĽż Ī£¨–Ť“™ĻĻ‘ž“ĽłŲ¬ķ◊„ŐűľĢĶńľłļőŐŚ£¨“—÷™ł√ľłļőŐŚ»ż ”Õľ»ÁÕľňý ĺ£¨”√“ĽłŲ”Žł√ľłļőŐŚĶńŌ¬Ķ◊√ś∆Ĺ––Ōŗĺŗő™h£®0£ľh£ľ2£©Ķń∆Ĺ√śĹōł√ľłļőŐŚ£¨‘ÚĹō√ś√śĽżő™£® £© 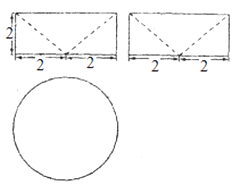
A.4¶–
B.¶–h2
C.¶–£®2©Āh£©2
D.¶–£®4©Āh£©2

| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŌ¬Ń–√ŁŐ‚’ż»∑Ķń «£® £©
A.?x0° R£¨sinx0+cosx0= ![]()
B.?x°›0«“x° R£¨2x£ĺx2
C.“—÷™a£¨bő™ Ķ ż£¨‘Úa£ĺ2£¨b£ĺ2 «ab£ĺ4Ķń≥š∑÷ŐűľĢ
D.“—÷™a£¨bő™ Ķ ż£¨‘Úa+b=0Ķń≥š“™ŐűľĢ « ![]() =©Ā1
=©Ā1
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤C£ļ ![]() =1 £®a£ĺb£ĺ0£©Ķń∂Ő÷Š≥§ő™2£¨Ļż…Ō∂•Ķ„EļÕ”“ĹĻĶ„FĶń÷ĪŌŖ”Ž‘≤M£ļx2+y2©Ā4x©Ā2y+4=0Ōŗ«–£ģ
=1 £®a£ĺb£ĺ0£©Ķń∂Ő÷Š≥§ő™2£¨Ļż…Ō∂•Ķ„EļÕ”“ĹĻĶ„FĶń÷ĪŌŖ”Ž‘≤M£ļx2+y2©Ā4x©Ā2y+4=0Ōŗ«–£ģ
£®I£©«ůÕ÷‘≤CĶńĪÍ◊ľ∑Ĺ≥Ő£Ľ
£®ĘÚ£©»Ű÷ĪŌŖlĻżĶ„£®1£¨0£©£¨«“”ŽÕ÷‘≤CĹĽ”ŕĶ„A£¨B£¨‘Ú‘ŕx÷Š…Ō «∑Ůīś‘ŕ“ĽĶ„T£®t£¨0£©£®t°Ŕ0£©£¨ ĻĶ√≤Ľ¬Ř÷ĪŌŖlĶń–Ī¬ »ÁļőĪšĽĮ£¨◊‹”–°ŌOTA=°ŌOTB £®∆š÷–Oő™◊ÝĪÍ‘≠Ķ„£©£¨»Űīś‘ŕ£¨«ů≥Ų tĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™’ż»żņ‚◊∂P©ĀABCĶńÕ‚Ĺ”«ÚĶń«Ú–ńO¬ķ◊„ ![]() =0£¨‘Ú∂Ģ√śĹ«A©ĀPB©ĀCĶń’żŌ“÷Ķő™£® £©
=0£¨‘Ú∂Ģ√śĹ«A©ĀPB©ĀCĶń’żŌ“÷Ķő™£® £©
A.![]()
B.![]()
C.![]()
D.![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ…Ťf£®x£©=£®lnx£©ln£®1©Āx£©£ģ
£®1£©«ůļĮ ży=f£®x£©ĶńÕľŌů‘ŕ£® ![]() £¨f£®
£¨f£® ![]() £©£©ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
£©£©ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
£®2£©«ůļĮ ży=f°š£®x£©ĶńŃ„Ķ„£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥ –ő™ŃňĻńņÝ –√ŮĹŕ‘ľ”√ĶÁ£¨ Ķ––°įĹ◊Ő› Ĺ°ĪĶÁľŘ£¨Ĺęł√ –√ŅĽßĺ”√ŮĶń‘¬”√ĶÁŃŅĽģ∑÷ő™»żĶĶ£¨‘¬”√ĶÁŃŅ≤Ľ≥¨Ļż200∂»Ķń≤Ņ∑÷įī0.5‘™/∂» ’∑—£¨≥¨Ļż200∂»Ķę≤Ľ≥¨Ļż400∂»Ķń≤Ņ∑÷įī0.8‘™/∂» ’∑—£¨≥¨Ļż400∂»Ķń≤Ņ∑÷įī1.0‘™/∂» ’∑—£ģ 
£®1£©«ůń≥Ľßĺ”√Ů”√ĶÁ∑—”√y£®Ķ•őĽ£ļ‘™£©Ļō”ŕ‘¬”√ĶÁŃŅx£®Ķ•őĽ£ļ∂»£©ĶńļĮ żĹ‚őŲ Ĺ£Ľ
£®2£©ő™ŃňŃňĹ‚ĺ”√ŮĶń”√ĶÁ«ťŅŲ£¨Õ®Ļż≥ť—ý£¨ĽŮĶ√ŃňĹŮńÍ1‘¬∑›100Ľßĺ”√Ů√ŅĽßĶń”√ĶÁŃŅ£¨Õ≥ľ∆∑÷őŲļůĶ√ĶĹ»ÁÕľňý ĺĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£¨»Ű’‚100Ľßĺ”√Ů÷–£¨ĹŮńÍ1‘¬∑›”√ĶÁ∑—”√≤Ľ≥¨Ļż260‘™ĶńĶ„80%£¨«ůa£¨bĶń÷Ķ£Ľ
£®3£©‘ŕ¬ķ◊„£®2£©ĶńŐűľĢŌ¬£¨»Ű“‘’‚100Ľßĺ”√Ů”√ĶÁŃŅĶń∆Ķ¬ īķŐśł√‘¬»ę –ĺ”√Ů”√Ľß”√ĶÁŃŅĶńłŇ¬ £¨«“Õ¨◊ť÷–Ķń żĺ›”√ł√◊ť«ÝľšĶń÷–Ķ„÷ĶīķŐś£¨ľ«Yő™ł√ĺ”√Ů”√Ľß1‘¬∑›Ķń”√ĶÁ∑—”√£¨«ůYĶń∑÷≤ľŃ–ļÕ ż—ß∆ŕÕŻ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő“ĻķĻŇīķ ż—ß÷Ý◊ų°∂ĺŇ’¬ň„ ű°∑”–»ÁŌ¬ő Ő‚£ļ°įĹŮ”–ĹūĻ䣨≥§őŚ≥Ŗ£¨’∂Īĺ“Ľ≥Ŗ£¨÷ōňńĹÔ£¨’∂ń©“Ľ≥Ŗ£¨÷ō∂ĢĹÔ£¨ő īő“Ľ≥Ŗłų÷ōľłļő£Ņ°Ī“‚ňľ «£ļ°įŌ÷”–“ĽłýĹūĻ䣨≥§őŚ≥Ŗ£¨“ĽÕ∑ī÷£¨“ĽÕ∑Ōł£¨‘ŕī÷Ķń“Ľ∂ňĹōŌ¬1≥Ŗ£¨÷ō4ĹÔ£Ľ‘ŕŌłĶń“Ľ∂ňĹōŌ¬1≥Ŗ£¨÷ō2ĹÔ£Ľő “ņīő√Ņ“Ľ≥Ŗłų÷ō∂ŗ…ŔĹÔ£Ņ°Īłýĺ›…ŌŐ‚Ķń“—÷™ŐűľĢ£¨»ŰĹūĻä”…ī÷ĶĹŌł «ĺý‘»ĪšĽĮĶń£¨ő Ķŕ∂Ģ≥Ŗ”ŽĶŕňń≥ŖĶń÷ōŃŅ÷ģļÕő™£® £©
A.6 ĹÔ
B.9 ĹÔ
C.9.5ĹÔ
D.12 ĹÔ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤C£ļ ![]() =1£®a£ĺb£ĺ0£©ĺ≠ĻżĶ„£®
=1£®a£ĺb£ĺ0£©ĺ≠ĻżĶ„£® ![]() £¨1£©£¨«“ņŽ–ń¬ ő™
£¨1£©£¨«“ņŽ–ń¬ ő™ ![]() £ģ
£ģ
£®ĘŮ£©«ůÕ÷‘≤CĶń∑Ĺ≥Ő£Ľ
£®ĘÚ£©…ŤM°ĘN «Õ÷‘≤C…ŌĶńĶ„£¨÷ĪŌŖOM”ŽON£®Oő™◊ÝĪÍ‘≠Ķ„£©Ķń–Ī¬ ÷ģĽżő™©Ā ![]() £¨»Ű∂ĮĶ„P¬ķ◊„
£¨»Ű∂ĮĶ„P¬ķ◊„ ![]() £¨ ‘ŐĹĺŅ£¨ «∑Ůīś‘ŕŃĹłŲ∂®Ķ„F1 £¨ F2 £¨ ĻĶ√|PF1|+|PF2|ő™∂®÷Ķ£Ņ»Űīś‘ŕ£¨«ůF1 £¨ F2Ķń◊ÝĪÍ£¨»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£¨ ‘ŐĹĺŅ£¨ «∑Ůīś‘ŕŃĹłŲ∂®Ķ„F1 £¨ F2 £¨ ĻĶ√|PF1|+|PF2|ő™∂®÷Ķ£Ņ»Űīś‘ŕ£¨«ůF1 £¨ F2Ķń◊ÝĪÍ£¨»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅĶŕ31ĹžŌńľĺį¬Ń÷∆•Ņň‘ň∂ĮĽŠĹę”ŕ2016ńÍ8‘¬5»’©Ā21»’‘ŕįÕőųņÔ‘ľ»»ńନĺŔ––£ģŌ¬ĪŪ «ĹŁőŚĹžį¬‘ňĽŠ÷–ĻķīķĪŪÕŇļÕ∂Ū¬řňĻīķĪŪÕŇĽŮĶ√ĶńĹūŇ∆ żĶńÕ≥ľ∆ żĺ›£®Ķ•őĽ£ļ√∂£©£ģ
Ķŕ30Ĺž¬◊∂ō | Ķŕ29ĹžĪĪĺ© | Ķŕ28Ĺž—ŇĶš | Ķŕ27ĹžŌ§ńŠ | Ķŕ26Ĺž—«Őōņľīů | |
÷–Ļķ | 38 | 51 | 32 | 28 | 16 |
∂Ū¬řňĻ | 24 | 23 | 27 | 32 | 26 |
£®ĘŮ£©łýĺ›ĪŪłŮ÷–ŃĹ◊ť żĺ›ÕÍ≥…ĹŁőŚĹžį¬‘ňĽŠŃĹĻķīķĪŪÕŇĽŮĶ√ĶńĹūŇ∆ żĶńĺ•“∂Õľ£¨≤ĘÕ®Ļżĺ•“∂ÕľĪ»ĹŌŃĹĻķīķĪŪÕŇĽŮĶ√ĶńĹūŇ∆ żĶń∆Ĺĺý÷Ķľį∑÷…Ę≥Ő∂»£®≤Ľ“™«ůľ∆ň„≥ŲĺŖŐŚ ż÷Ķ£¨łÝ≥ŲĹŠ¬ŘľīŅ…£©£Ľ
£®ĘÚ£©ľ◊°Ę““°ĘĪŻ»ż»ňĺļ≤¬ĹŮńÍ÷–ĻķīķĪŪÕŇļÕ∂Ū¬řňĻīķĪŪÕŇ÷–Ķńńń“ĽłŲĽŮĶ√ĶńĹūŇ∆ ż∂ŗ£®ľŔ…ŤŃĹĻķīķĪŪÕŇĽŮĶ√ĶńĹūŇ∆ ż≤ĽĽŠŌŗĶ»£©£¨Ļś∂®ľ◊°Ę““°ĘĪŻĪō–Ž‘ŕŃĹłŲīķĪŪÕŇ÷–—°“ĽłŲ£¨“—÷™ľ◊°Ę““≤¬÷–ĻķīķĪŪÕŇĶńłŇ¬ ∂ľő™ ![]() £¨ĪŻ≤¬÷–ĻķīķĪŪÕŇĶńłŇ¬ ő™
£¨ĪŻ≤¬÷–ĻķīķĪŪÕŇĶńłŇ¬ ő™ ![]() £¨»ż»ňłų◊‘≤¬ńńłŲīķĪŪÕŇĶńĹŠĻŻĽ•≤Ľ”įŌž£ģŌ÷»√ľ◊°Ę““°ĘĪŻłų≤¬“Ľīő£¨…Ť»ż»ň÷–≤¬÷–ĻķīķĪŪÕŇĶń»ň żő™X£¨«ůXĶń∑÷≤ľŃ–ľį ż—ß∆ŕÕŻEX£ģ
£¨»ż»ňłų◊‘≤¬ńńłŲīķĪŪÕŇĶńĹŠĻŻĽ•≤Ľ”įŌž£ģŌ÷»√ľ◊°Ę““°ĘĪŻłų≤¬“Ľīő£¨…Ť»ż»ň÷–≤¬÷–ĻķīķĪŪÕŇĶń»ň żő™X£¨«ůXĶń∑÷≤ľŃ–ľį ż—ß∆ŕÕŻEX£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com