
已知函数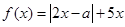 ,其中实数
,其中实数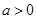 .
.
(1)当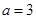 时,求不等式
时,求不等式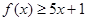 的解集;
的解集;
(2)若不等式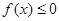 的解集为
的解集为 ,求
,求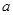 的值.
的值.
(1)不等式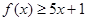 的解集为
的解集为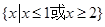 ;(2)
;(2)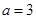
解析试题分析:(1)将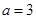 代入
代入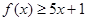 得一绝对值不等式:
得一绝对值不等式: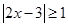 ,解此不等式即可.
,解此不等式即可.
(2)含绝对值的不等式,一般都去掉绝对值符号求解。本题有以下三种考虑:
思路一、根据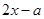 的符号去绝对值.
的符号去绝对值. 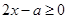 时,
时,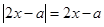 ,所以原不等式转化为
,所以原不等式转化为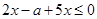 ;
;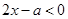 时,
时,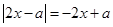 ,所以原不等式转化为
,所以原不等式转化为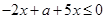
思路二、利用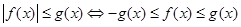 去绝对值.
去绝对值. 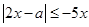 ,此不等式化等价于
,此不等式化等价于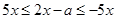 .
.
思路三、从不等式与方程的关系的角度突破.本题是含等号的不等式,所以可取等号从方程入手.
试题解析:(1)当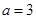 时,
时,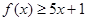 可化为
可化为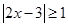 ,由此可得
,由此可得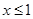 或
或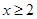
故不等式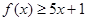 的解集为
的解集为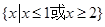 5分
5分
(2)法一:(从去绝对值的角度考虑)
由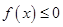 ,得
,得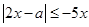 ,此不等式化等价于
,此不等式化等价于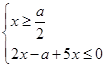 或
或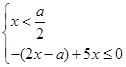
解之得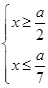 或
或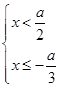 ,
,
因为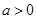 ,所以不等式组的解集为
,所以不等式组的解集为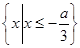 ,由题设可得
,由题设可得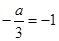 ,故
,故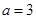 10分
10分
法二:(从等价转化角度考虑)
由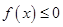 ,得
,得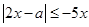 ,此不等式化等价于
,此不等式化等价于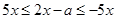 ,
,
即为不等式组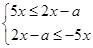 ,解得
,解得 ,
,
因为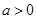 ,所以不等式组的解集为
,所以不等式组的解集为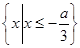 ,由题设可得
,由题设可得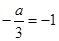 ,故
,故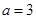 10分
10分
法三:(从不等式与方程的关系角度突破)
因为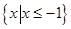 是不等式
是不等式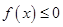 的解集,所以
的解集,所以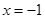 是方程
是方程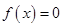 的根,
的根,
把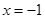 代入
代入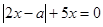 得
得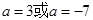 ,因为
,因为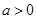 ,所以
,所以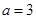 10分
10分
考点:1、绝对值的意义;2、含绝对值不等式的解法;3、含参数不等式的解法


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com