
【题目】为了调查生活规律与患胃病是否与有关,某同学在当地随机调查了200名30岁以上的人,并根据调查结果制成了不完整的列联表如下:
不患胃病 | 患胃病 | 总计 | |
生活有规律 | 60 | 40 | |
生活无规律 | 60 | 100 | |
总计 | 100 |
(1)补全列联表中的数据;
(2)用独性检验的基本原理,说明生活无规律与患胃病有关时,出错的概率不会超过多少?
参考公式和数表如下:
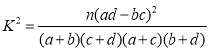
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|,不等式f(x)≤4的解集为{x|-2≤x≤6}.
(1)求实数a的值;
(2)设g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根据上表的数据得到如下的散点图.
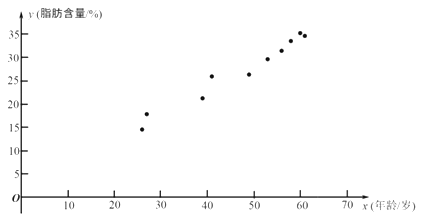
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
附:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数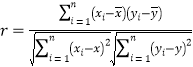
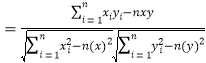
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为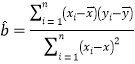 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.乘坐高铁可以网络购票,为了研究网络购票人群的年龄分布情况,在5月31日重庆到成都高铁9600名网络购票的乘客中随机抽取了120人进行了统计并记录,按年龄段将数据分成6组:![]() ,得到如图所示的直方图:
,得到如图所示的直方图:
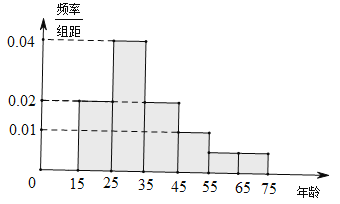
(1)若从总体的9600名网络购票乘客中随机抽取一人,估计其年龄大于35岁的概率;
(2)试估计总体中年龄在区间![]() 内的人数;
内的人数;
(3)试通过直方图,估计5月31日当天网络购票的9600名乘客年龄的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户计划种植莴笋和西红柿,种植面积不超过![]() 亩,投入资金不超过
亩,投入资金不超过![]() 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为____万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:
(1)命题“![]() ,
,![]() ”的否定形式是“
”的否定形式是“![]() ,
,![]() ”;
”;
(2)已知![]() ,则
,则![]() ;
;
(3)已知回归直线的斜率的估计值是2,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() ;
;
(4)对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大;
有关系”的把握越大;
(5)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变.
其中正确说法的个数为( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为发展业务,某调研组对![]() ,
,![]() 两个公司的产品需求量进行调研,准备从国内
两个公司的产品需求量进行调研,准备从国内![]() 个人口超过
个人口超过![]() 万的超大城市和
万的超大城市和![]() (
(![]() )个人口低于
)个人口低于![]() 万的小城市随机抽取若干个进行统计,若一次抽取
万的小城市随机抽取若干个进行统计,若一次抽取![]() 个城市,全是小城市的概率为
个城市,全是小城市的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若一次抽取![]() 个城市,则:①假设取出小城市的个数为
个城市,则:①假设取出小城市的个数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
②若取出的![]() 个城市是同一类城市,求全为超大城市的概率.
个城市是同一类城市,求全为超大城市的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆与抛物线![]() 有一个相同的焦点,且该椭圆的离心率为
有一个相同的焦点,且该椭圆的离心率为![]() ,
,
(Ⅰ)求该椭圆的标准方程:
(Ⅱ)求过点![]() 的直线与该椭圆交于A,B两点,O为坐标原点,若
的直线与该椭圆交于A,B两点,O为坐标原点,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com