
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据算法的定义:在数学中,算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.现在,算法通常可以编成计算机程序,让计算机执行并解决问题.简化后可得:算法是步骤,故判断语句是否是算法,就是看语句表达的事件,是否有步骤.
解答 解:①求过M(1,2)与N(-3,-4)两点的直线方程可先求直线MN的斜率,再利用点斜式方程求得,是算法;
②求以A(2,2),B(2,6),C(4,4)为顶点的△ABC的面积可先求AB的长a,再求直线AB的方程及点C到AB的距离h,最后利用S=$\frac{1}{2}$ah进行计算,是算法;
③判断方程x2+x+1=0有无实数根,是算法;
④植树需要运苗、挖坑、栽苗、浇水这些步骤,是算法.
故选D.
点评 在数学中,算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.现在,算法通常可以编成计算机程序,让计算机执行并解决问题.简化后可得:算法是步骤,故判断语句是否是算法,就是看语句表达的事件,是否有步骤.


科目:高中数学 来源: 题型:解答题
 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠CAB的角平分线AE交BC和圆O于点D、E,且PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠CAB的角平分线AE交BC和圆O于点D、E,且PA=2PB=10.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
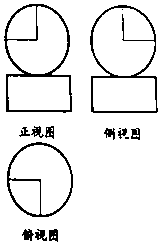 如图,是某几何体的三视图,其中矩形的高为圆的半径,若该几何体的体积是$\frac{52π}{3}$,则此几何体的表面积为( )
如图,是某几何体的三视图,其中矩形的高为圆的半径,若该几何体的体积是$\frac{52π}{3}$,则此几何体的表面积为( )| A. | 33π | B. | 34π | C. | 36π | D. | 42π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
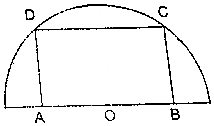 如图所示,有一块半径为2的半圆形钢板,设计剪裁成矩形ABCD的形状,它的边AB在圆O的直径上,边CD的端点在圆周上,若设矩形的边AD为x;
如图所示,有一块半径为2的半圆形钢板,设计剪裁成矩形ABCD的形状,它的边AB在圆O的直径上,边CD的端点在圆周上,若设矩形的边AD为x;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com