
分析 (Ⅰ)求出f(x)的导数,由两直线平行的条件:斜率相等,可得m的方程,可得m的值,求得f(x)的导数,即可判断f(x)的单调性;
(Ⅱ)不等式f(x)≥1即$2lnx+\frac{m}{x+1}≥1$,由x的范围,运用参数分离,求得右边函数的最大值,即可得到所求m的范围.
解答 解:(Ⅰ)f(x)定义域是(0,+∞),导数$f'(x)=\frac{2}{x}-\frac{m}{{{{(x+1)}^2}}}$,
依题意f'(1)=1,即2-$\frac{m}{4}$=1,解得m=4,
则$f'(x)=\frac{{2({x^2}+1)}}{{x{{(x+1)}^2}}}>0$,所以函数f(x)在(0,+∞)单调增加;…(6分)
(Ⅱ)不等式f(x)≥1即$2lnx+\frac{m}{x+1}≥1$,
因为x≥1,所以m≥x+1-2(x+1)lnx,
设g(x)=x+1-2(x+1)lnx,导数$g'(x)=-\frac{2xlnx+x+2}{x}$,
当x≥1时,g'(x)≤0,g(x)在[1,+∞)单调递减,
所以当x≥1时,g(x)≤g(1)=2,因此m≥2,
实数m的取值范围是[2,+∞).…(12分)
点评 本题考查导数的运用:求切线的斜率和单调区间,考查函数的单调性及应用,以及参数分离和恒成立问题的解法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
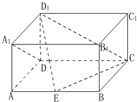 如图,在长方体ABCD-A1B1C1D1中,AD=DD1=1,DC=2,E为AB上一点.
如图,在长方体ABCD-A1B1C1D1中,AD=DD1=1,DC=2,E为AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{3}$ | B. | $x=\frac{2π}{3}$ | C. | $x=\frac{5π}{12}$ | D. | $x=\frac{7π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com