
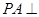 平面
平面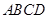 ,四边形
,四边形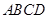 为正方形,且
为正方形,且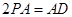 ,
,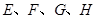 分别是线段
分别是线段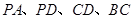 的中点.
的中点.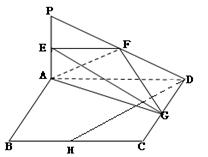
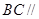 平面
平面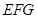 ;
;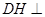 平面
平面 ;
;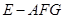 与四棱锥
与四棱锥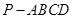 的体积比.
的体积比.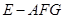 与四棱锥
与四棱锥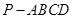 的体积比
的体积比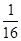
 ,
, ,从而有
,从而有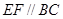 ,然后由直线和平面平行的判定定理可得
,然后由直线和平面平行的判定定理可得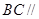 平面
平面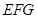 ;(Ⅱ)利用直线和平面垂直的性质定理可得AE⊥DH,再证DH⊥AG,由直线和平面垂直的判定定理可得
;(Ⅱ)利用直线和平面垂直的性质定理可得AE⊥DH,再证DH⊥AG,由直线和平面垂直的判定定理可得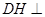 平面
平面 ;(Ⅲ)由已知可得
;(Ⅲ)由已知可得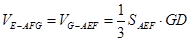 ,
,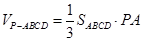 ,所以
,所以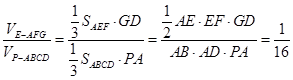 ,此问注意直线和平面关系的运用和体积的转化.
,此问注意直线和平面关系的运用和体积的转化.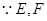 分别为
分别为 中点,所以AD∥EF,∵BC∥AD, ,∴BC∥EF....2分
中点,所以AD∥EF,∵BC∥AD, ,∴BC∥EF....2分
 ∥平面EFG............4分
∥平面EFG............4分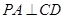 ,又
,又 ,所以
,所以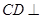 平面
平面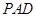 ,
,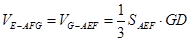 ,
,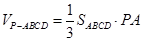
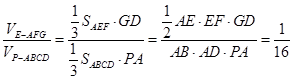 .........12分
.........12分

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
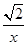 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.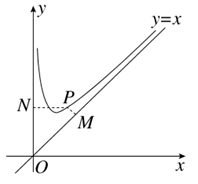
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com