
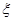 ,求
,求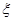 的分布列及数学期望.
的分布列及数学期望. 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
 (如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为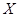 ,若
,若 就去打球,若
就去打球,若 就去唱歌,若
就去唱歌,若 就去下棋。
就去下棋。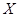 的所有可能值;
的所有可能值;
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 | x | 0.45 |
| 10 | 35 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 | z | |
| 10 | | 0.35 |
| 合计 | 80 | 1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
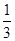 .那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
.那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com