
 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准,为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:),样本统计结果如图表:
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准,为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:),样本统计结果如图表:| 分组 | 频数 | 频率 |
| [0,1) | a | |
| [1,2) | 0.19 | |
| [2,3) | 50 | b |
| [3,4) | 0.23 | |
| [4,5) | 0.18 | |
| [5,6) | 5 |
分析 (I)从直方图中得在[2,3)小组中的频率,利用频率分布直方图中$\frac{50}{n}$=b=0.25,求出b,再利用样本容量等于频数除以频率得出n,最后求出a处的数;
(II)利用列举法确定基本事件的个数,根据古典概率计算公式计算即可.
解答 解:(Ⅰ)由频率分布直方图得月均用水量在[2,3)小组中的频率为0.25×1=0.25,即b=0.25------(2分)
又∵$\frac{50}{n}$=b=0.25,∴n=200-----(4分)
∴a=$\frac{25}{200}$=0.125-------(6分)
(Ⅱ)记样本中月均用水量在[5,6](单位:t)的5位居民为a,b,c,d,e,且不妨设e为月均用水量最多的居民.记月均用水量最多的居民被选中为事件A,所以基本事件为:(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e)共计10个基本事件-----(8分)
事件A包含的基本事件有(a,e),(b,e),(c,e),(d,e),共4个-----(10分)
所以月均用水量最多的居民被选中概率P(A)=0.4---(12分)
点评 用样本估计总体,是研究统计问题的一个基本思想方法.频率分布直方图中小长方形的面积=组距×$\frac{频率}{组距}$=频率,各个矩形面积之和等于1,能根据直方图求频率,属于常规题型.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
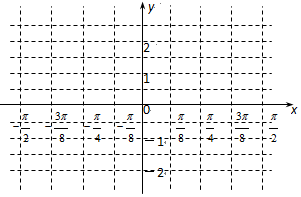 已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.
已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com