
| A. | 200 | B. | 350 | C. | 400 | D. | 500 |
分析 设A药品为x箱,B药品为y箱,该企业捐献给医院的两种药品总箱数为z=x+y,则x,y满足的关系式为$\left\{\begin{array}{l}{0.15x+0.3y≤100}\\{x≥100}\\{y≥100}\\{y≥x}\end{array}\right.$,根据约束条件对目标函数的范围进行验证即可
解答 解:设A药品为x箱,B药品为y箱,该企业捐献给医院的两种药品总箱数为z=x+y,
则x,y满足的关系式为$\left\{\begin{array}{l}{0.15x+0.3y≤100}\\{x≥100}\\{y≥100}\\{y≥x}\end{array}\right.$,
若x+y=500,又因为≥x,∴y≥250,
则0.15x+0.3y=0.15(500-y)+0.3y=75+0.15y>100,不合题意.
若x+y=400,又因为y≥x,∴y≥200,
则0.15x+0.3y=0.15(400-y)+0.3y=60+0.15y≥90,合题意.
故选:C
点评 本题考查了一次函数的值域问题,转化思想是解题关键,属于中档题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
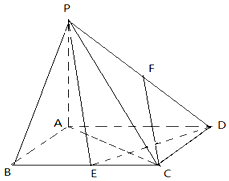 如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果平面α外的直线a不平行于平面α,平面α内不存在与a平行的直线 | |
| B. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么直线l⊥平面γ | |
| C. | 如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β | |
| D. | 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6+4\sqrt{3}$ | B. | $8+2\sqrt{3}$ | C. | $4+6\sqrt{3}$ | D. | $8+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
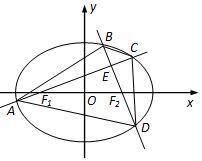 已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.
已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com