
分析 (1)设x>0,则-x<0,利用已知函数解析式和函数的奇偶性可得x>0时的解析式,则答案可求;
(2)求出函数g(x),找出对称轴方程,对a分类求得函数的最小值;
(3)把f(x)≤-2at+4对于任意的x∈[-1,1],a∈[-1,1]恒成立,转化为0≤-2at+4,进一步转化为关于t的不等式组得答案.
解答 解:(1)设x>0,则-x<0,
又函数f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=(-x)2-2x=x2-2x.
∴$f(x)=\left\{\begin{array}{l}{x^2}-2x,x>0\\{x^2}+2x,x≤0.\end{array}\right.$;
(2)g(x)=f(x)+(4-2a)x+2=x2+2x-2ax+2(1≤x≤2),对称轴方程为:x=a-1,
当a-1≤1 时,g(1)=5-2a为最小;
当1<a-1≤2时,g(a-1)=-a2+2a+1为最小;
当a-1>2时,g(2)=10-4a为最小.
综上:h(a)=$\left\{\begin{array}{l}{5-2a,a≤2}\\{-{a}^{2}+2a+1,2<a≤3}\\{10-4a,a>3}\end{array}\right.$;
(3)f(x)≤-2at+4对于任意的x∈[-1,1],a∈[-1,1]恒成立,
即0≤-2at+4,也就是2ta-4≤0,a∈[-1,1]恒成立,
∴$\left\{\begin{array}{l}{-2t-4≤0}\\{2t-4≤0}\end{array}\right.$,解得:-2≤t≤2.
点评 本题考查函数解析式的求解及常用方法,考查数学转化思想方法,训练了恒成立问题的求解方法,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 200 | B. | 350 | C. | 400 | D. | 500 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 成绩分数 | [0,70] | [70,90] | [90,100] |
| 等级 | C级 | B级 | A级 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧(¬q) | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
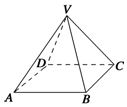 如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com