
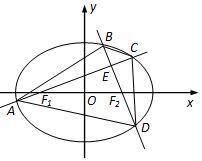
 已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.
已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.分析 (Ⅰ)由椭圆的定义及焦距|F1F2|=2c=2,求得a和c的值,则b2=a2-c2=2,即可求得椭圆的方程及离心率.
(Ⅱ)当直线的斜率不存在时,由S=$\frac{1}{2}$丨AC丨•丨BD丨=4,当直线斜率存在时,设直线方程,代入椭圆方程,由韦达定理及弦长公式分别求得丨AC丨,丨BD丨根据函数的单调性即可求得四边形ABCD面积的最大值.
解答 解:(Ⅰ)由题意可知:|F1F2|=2c=2,c=1,2a=|PF1|+|PF2|=2$\sqrt{3}$,a=$\sqrt{3}$,
b2=a2-c2=2,离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,
∴椭圆的标准方程为:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$;
(Ⅱ)当直线l2⊥l1,当斜率不存在时,EF1⊥EF2,此时求得丨EO丨=$\frac{1}{2}$丨F1F2丨=1,
∴E点轨迹为以原点为圆心,半径为1的圆,显然点E在椭圆W上内部,
∴四边形ABCD面积S=S△ABC+S△ADC=$\frac{1}{2}$丨AC丨•丨BE丨+$\frac{1}{2}$丨AC丨•丨DE丨=$\frac{1}{2}$丨AC丨•丨BD丨,
将x=-1代入椭圆方程,求得y=±$\frac{2\sqrt{3}}{3}$,此时丨BD丨=$\frac{4\sqrt{3}}{3}$,丨AC丨=2$\sqrt{3}$,
则四边形ABCD面积S=$\frac{1}{2}$丨AC丨•丨BD丨=4,
当直线l2,l1都存在时,设直线l1,x=my-1,(m≠0),
设A(x1,y1),B(x2,y2),
$\left\{\begin{array}{l}{x=my-1}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,整理得:(2m2+3)y2-4my-4=0,
则y1+y2=$\frac{4m}{2{m}^{2}+3}$,y1y2=-$\frac{4}{2{m}^{2}+3}$,
则丨AC丨=$\sqrt{1+{m}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{4\sqrt{3}({m}^{2}+1)}{2{m}^{2}+3}$,
同理直线l1,x=-$\frac{1}{m}$x+1,同理求得丨BD丨=$\frac{4\sqrt{3}({m}^{2}+1)}{2+3{m}^{2}}$,
∴四边形ABCD面积S=$\frac{1}{2}$丨AC丨•丨BD丨=$\frac{1}{2}$×$\frac{4\sqrt{3}({m}^{2}+1)}{2{m}^{2}+3}$×$\frac{4\sqrt{3}({m}^{2}+1)}{2+3{m}^{2}}$,
=$\frac{24({m}^{2}+1)^{2}}{(2{m}^{2}+3)(3{m}^{2}+2)}$,
=$\frac{24({m}^{4}+2{m}^{2}+1)}{6{m}^{4}+13{m}^{2}+6}$=4×$\frac{6{m}^{4}+12{m}^{2}+6}{6{m}^{4}+13{m}^{2}+6}$,
=4(1-$\frac{{m}^{2}}{6{m}^{4}+13{m}^{2}+6}$)<4,
综上可知四边形ABCD面积的最大值4,此时直线l2,l1一条为椭圆的长轴,一条与x轴垂直.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,考查韦达定理,弦长公式,考查函数的单调性及椭圆的综合应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 200 | B. | 350 | C. | 400 | D. | 500 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )| A. | 36πcm2 | B. | 64πcm2 | C. | 80πcm2 | D. | 100πcm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 成绩分数 | [0,70] | [70,90] | [90,100] |
| 等级 | C级 | B级 | A级 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
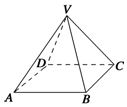 如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com