
分析 (Ⅰ)由椭圆经过点$(0,\sqrt{2})$,且离心率为$\frac{{\sqrt{2}}}{2}$,列出方程给求出a,b,由此能求出椭圆C的方程.
(Ⅱ)设P(x0,y0),M(x1,y1),N(x2,y2),当M(x1,y1),N(x2,y2)在x轴同侧,不妨设x1>0,x2<0,y1>0,y2>0,推导出${y}_{1}=\frac{{y}_{0}}{{x}_{0}+2}{x}_{1}$,${y}_{2}=\frac{{y}_{0}}{{x}_{0}-2}{x}_{2}$,且$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{2}=1$,过M,N作x轴的垂线,垂足分别为M′,N′,${S}_{△OMN}={S}_{四边形M{M}^{'}{N}^{'}N}$-${S}_{△OM{M}^{'}}-{S}_{△ON{N}^{'}}$=-${x}_{1}{x}_{2}•\frac{1}{{y}_{0}}$,由$\left\{\begin{array}{l}{\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{2}=1}\\{{y}_{1}=\frac{{y}_{0}}{{x}_{0}+2}{x}_{1}}\end{array}\right.$,得${{x}_{1}}^{2}+2(\frac{{y}_{0}}{{x}_{0}+2}{x}_{1})^{2}=4$,由此求出${S}_{△OMN}=\sqrt{2}$.当M(x1,y1),N(x2,y2)在x轴异侧,同理得${S}_{△OMN}=\sqrt{2}$,由此能证明△OMN的面积为定值$\sqrt{2}$.
解答 解:(Ⅰ)∵椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点$(0,\sqrt{2})$,且离心率为$\frac{{\sqrt{2}}}{2}$,
∴$\left\{\begin{array}{l}{b=\sqrt{2}}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=$\sqrt{2}$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
证明:(Ⅱ)设P(x0,y0),M(x1,y1),N(x2,y2),
①M(x1,y1),N(x2,y2)在x轴同侧,不妨设x1>0,x2<0,y1>0,y2>0,
射线OM的方程为y=$\frac{{y}_{0}}{{x}_{0}+2}x$,射线ON的方程为y=$\frac{{y}_{0}}{{x}_{0}-2}x$,
∴${y}_{1}=\frac{{y}_{0}}{{x}_{0}+2}{x}_{1}$,${y}_{2}=\frac{{y}_{0}}{{x}_{0}-2}{x}_{2}$,且$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{2}=1$,
过M,N作x轴的垂线,垂足分别为M′,N′,
${S}_{△OMN}={S}_{四边形M{M}^{'}{N}^{'}N}$-${S}_{△OM{M}^{'}}-{S}_{△ON{N}^{'}}$
=$\frac{1}{2}[({y}_{1}+{y}_{2})({x}_{1}-{x}_{2})-{x}_{1}{y}_{1}+{x}_{2}{y}_{2}]$
=$\frac{1}{2}({x}_{1}{y}_{2}-{x}_{2}{y}_{1})=\frac{1}{2}({x}_{1}•\frac{{y}_{0}{x}_{2}}{{x}_{0}-2}{-x}_{2}•\frac{{y}_{0}{x}_{1}}{{x}_{0}+2})$
=$\frac{1}{2}{x}_{1}{x}_{2}•\frac{4{y}_{0}}{{{x}_{0}}^{2}-4}$=$\frac{1}{2}{x}_{1}{x}_{2}•\frac{4{y}_{0}}{-2{y}_{0}}$=-${x}_{1}{x}_{2}•\frac{1}{{y}_{0}}$,
由$\left\{\begin{array}{l}{\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{2}=1}\\{{y}_{1}=\frac{{y}_{0}}{{x}_{0}+2}{x}_{1}}\end{array}\right.$,得${{x}_{1}}^{2}+2(\frac{{y}_{0}}{{x}_{0}+2}{x}_{1})^{2}=4$,
即${{x}_{1}}^{2}=\frac{4({x}_{0}+2)^{2}}{({x}_{0}+2)^{2}+2{{y}_{0}}^{2}}$=$\frac{4({x}_{0}+2)^{2}}{({x}_{0}+2)^{2}+4-{{x}_{0}}^{2}}$=2+x0,
同理,${{x}_{2}}^{2}$=2-x0,∴${{x}_{1}}^{2}{{x}_{2}}^{2}$=4-${{x}_{0}}^{2}$=2${{y}_{0}}^{2}$,即${x}_{1}{x}_{2}=-\sqrt{2}{y}_{0}$,
∴${S}_{△OMN}=\sqrt{2}$.
②M(x1,y1),N(x2,y2)在x轴异侧,同理①得${S}_{△OMN}=\sqrt{2}$,
综合①②,△OMN的面积为定值$\sqrt{2}$.
点评 本题考查椭圆方程的求法,考查三角形面积为定值的证明,考查椭圆、直线与椭圆位置关系的应用,考查推理论证能力、运算求解能力,考查数形结合思想、转化化归思想,是中档题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | x2+y2-4x+2y+4=0 | B. | x2+y2-4x-2y-4=0 | C. | x2+y2-4x+2y-4=0 | D. | x2+y2+4x+2y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6+4\sqrt{3}$ | B. | $8+2\sqrt{3}$ | C. | $4+6\sqrt{3}$ | D. | $8+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
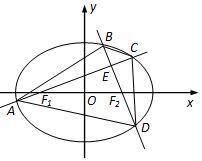 已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.
已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=lnx | B. | y=x+$\frac{1}{x}$ | C. | y=x2 | D. | $y={x^{\frac{1}{3}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com