
分析 求出抛物线的准线方程,求出双曲线的焦点坐标,利用双曲线的渐近线方程,求出实半轴与虚半轴的长,得到双曲线方程即可.
解答 解:抛物线y2=16x的准线x=-4过双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一个焦点(-4,0),
双曲线的一条渐近线为$y=\sqrt{3}x$,可得b=$\sqrt{3}a$,c=$\sqrt{{a}^{2}+{b}^{2}}=4$,
解得a=2,b=2$\sqrt{3}$,
所求双曲线方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$.
故答案为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$.
点评 本题考查双曲线方程的求法,抛物线的简单性质以及双曲线的简单性质的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
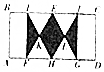 如图所示,已知长方形ABCD中,BC=2AB,△EFG与△HIJ均为等边三角形,F、H、G在AD上,I、E、J在BC上,连接FI,GJ,且AB∥FI∥GJ,若AF=GD,则向长方形ABCD内投掷一个点,该点落在阴影区域内的概率为$\frac{\sqrt{3}}{6}$.
如图所示,已知长方形ABCD中,BC=2AB,△EFG与△HIJ均为等边三角形,F、H、G在AD上,I、E、J在BC上,连接FI,GJ,且AB∥FI∥GJ,若AF=GD,则向长方形ABCD内投掷一个点,该点落在阴影区域内的概率为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 成绩分数 | [0,70] | [70,90] | [90,100] |
| 等级 | C级 | B级 | A级 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com