
已知幂函数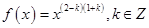 ,且
,且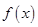 在
在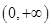 上单调递增.
上单调递增.
(1)求实数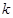 的值,并写出相应的函数
的值,并写出相应的函数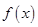 的解析式;
的解析式;
(2)若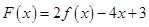 在区间
在区间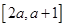 上不单调,求实数
上不单调,求实数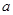 的取值范围;
的取值范围;
(3)试判断是否存在正数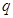 ,使函数
,使函数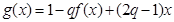 在区间
在区间 上的值域为
上的值域为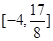 若存在,求出
若存在,求出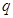 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) 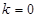 或
或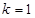 ,
,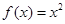 (2)
(2) 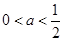 (3)
(3) 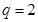
【解析】
试题分析:(1)由题意知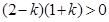 ,解得:
,解得: . 2分
. 2分
又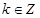 ∴
∴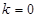 或
或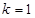 ,
3分
,
3分
分别代入原函数,得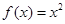 .
4分
.
4分
(2)由已知得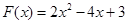 .
5分
.
5分
要使函数不单调,则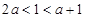 ,则
,则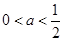 .
8分
.
8分
(3)由已知,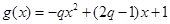 . 9分
. 9分
法一:假设存在这样的正数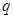 符合题意,
符合题意,
则函数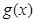 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为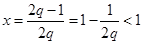 ,
,
因而,函数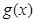 在
在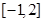 上的最小值只能在
上的最小值只能在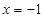 或
或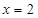 处取得,
处取得,
又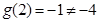 ,
,
从而必有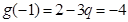 ,解得
,解得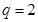 .
.
此时,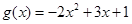 ,其对称轴
,其对称轴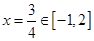 ,
,
∴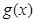 在
在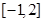 上的最大值为
上的最大值为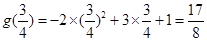 ,符合题意.
,符合题意.
∴存在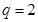 ,使函数
,使函数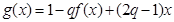 在区间
在区间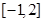 上的值域为
上的值域为 14分法二:假设存在这样的正数
14分法二:假设存在这样的正数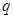 符合题意,
符合题意,
由(1)知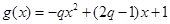 ,
,
则函数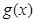 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为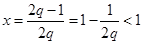 ,
,

考点:幂函数及二次函数单调性最值
点评:第二问中二次函数不单调需满足对称轴在给定区间内,第三问关于最值的考查需注意对称轴与给定区间的关系,从而确定给定区间上的单调性得到最值,一般求解时都要分情况讨论


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省吉安市白鹭洲中学高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
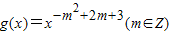 为偶函数,且在区间(0,+∞)上是单调增函数,又f(x)=sinx+mcosx,F(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的导函数.
为偶函数,且在区间(0,+∞)上是单调增函数,又f(x)=sinx+mcosx,F(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的导函数.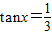 ,求F(x)的值;
,求F(x)的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com