
分析 由对任意的x∈R,f(x+2)=$\frac{1}{f(x)}$得函数的周期性为4,根据函数的奇偶性和周期性进行转化即可得到结论.
解答 解:∵对任意的x∈R,f(x+2)=$\frac{1}{f(x)}$,
∴f(x+4)=f(x),
∴函数的周期是4,
∴f(2017)=f(1),f(2015)=f(-1)
∵f(x)是定义在R上的奇函数,
∴f(1)=-f(-1),
∵当x∈[-2,0)时,f(x)=log2(x+3),
∴f(-1)=log22=1,
则f(2017)-f(2015)=-1-1=-2,
故答案为:-2
点评 本题主要考查函数值的计算,根据函数的奇偶性和周期性进行转化是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 11 | C. | 14 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,BC=$\sqrt{2}$,F为BE的中点.
如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,BC=$\sqrt{2}$,F为BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
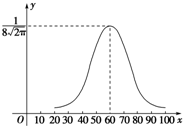 某县10000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(52,68]的人数大约是6820.
某县10000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(52,68]的人数大约是6820.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com