Question

（本题14分）如图,一水渠的横断面是抛物线形，O是抛物线的顶点,口宽EF=4米，高3米，建立适当的直角坐标系，（1）求抛物线方程.（2）若将水渠横断面改造成等腰梯形ABCD，要求高度不变，只挖土，不填土，求梯形ABCD的下底AB多大时，所挖的土最少？

 

Answer 1

【答案】

（1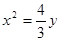）；(2)梯形ABCD的下底AB=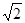米时，所挖的土最少.

【解析】

试题分析：（1）解：如图 以O为原点，AB所在的直线为X轴，建立平面直角坐标系，

则F（2，3），设抛物线的方程是

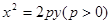
因为点F在抛物线上，所以

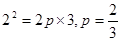
所以抛物线的方程是

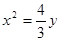 ……………………4分

(2) 解：等腰梯形ABCD中,AB∥CD，线段AB的中点O是抛物线的顶点，AD，AB，BC分别与抛物线切于点M，O，N

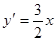，设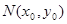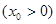，，则抛物线在N处的切线方程是……………………8分

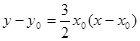，所以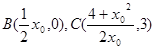，……………………10分

梯形ABCD的面积是

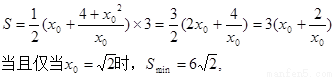…………………12分

答：梯形ABCD的下底AB=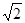米时，所挖的土最少. ……………………14分

考点：本题主要考查抛物线在实际问题中的应用，导数的几何意义，均值定理的应用，直线与抛物线的位置关系。

点评：综合题，通过建立适当的直角坐标系，求得抛物线方程，从而通过研究直线与抛物线的位置关系，求切线方程，确定得到截面面积表达式，运用均值定理求得最值。