
给出以下五个命题:
① ,若
,若 ,则
,则 或
或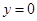 的否命题是假命题;
的否命题是假命题;
②函数 的最小值为2;
的最小值为2;
③若函数 的图象关于点(1,0)对称,则
的图象关于点(1,0)对称,则 的值为-3;
的值为-3;
④若 ,则函数
,则函数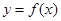 是以4为周期的周期函数;
是以4为周期的周期函数;
⑤若(1+x)10 =a0+a1x+a2x2 +… +a10x10,则a0+a1 +2a2+3a3 +… +10a10=10×29.
其中真命题的序号是___________.
①③④
解析试题分析:对于①,x,y∈R,若x2+y2=0,则x=0或y=0的否命题是若x2+y2≠0,则x,y全不为零,不正确,故是假命题,故①正确;对于②,函数y=3x+3-x(x<0)的最小值为2此时3x=1,此时x=0,但取不到,故②不正确;对于③,函数f(x)=x3+ax2+2的图象关于点(1,0)对称,则f(1+x)+f(1-x)=0,解得a=-3,故③正确;对于④,∵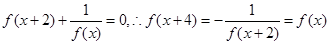 ,故函数y=f(x)是以4为周期的周期函数,故④正确;对于⑤,令x=0解得a0=1,对等式两边取导数得10(1+x)9=a1+2a2x+3a3x2+…+10a10x9,
,故函数y=f(x)是以4为周期的周期函数,故④正确;对于⑤,令x=0解得a0=1,对等式两边取导数得10(1+x)9=a1+2a2x+3a3x2+…+10a10x9,
令x=1得a1+2a2+3a3+…+10a10=10×29,∴a0+a1+2a2+3a3+…+10a10=10×29+1,故不正确;
故答案为:①③④
考点:命题的真假判断与应用;四种命题;函数的周期性;二项式定理.
点评:本题主要考查了命题的真假判断,以及函数的周期性,对称性和二项式定理的应用,同时考查了运算求解的能力,属于基础题.


科目:高中数学 来源: 题型:填空题
已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的________条件.(填充分必要条件,充分不必要条件,必要不充分条件,既不充分又不必要条件之一)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列命题:
①存在实数 ,使得
,使得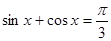 ;
;
②函数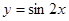 的图象向右平移
的图象向右平移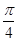 个单位,得到
个单位,得到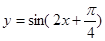 的图象;
的图象;
③函数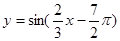 是偶函数;
是偶函数;
④已知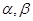 是锐角三角形ABC的两个内角,则
是锐角三角形ABC的两个内角,则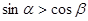 。
。
其中正确的命题的个数为
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列命题:
①函数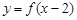 与函数
与函数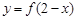 的图象关于
的图象关于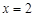 对称
对称
②函数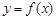 导函数为
导函数为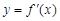 ,若
,若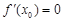 ,则
,则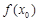 必为函数
必为函数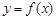 的极值.
的极值.
③函数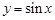 在一象限单调递增
在一象限单调递增
④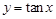 在其定义域内为单调增函数.
在其定义域内为单调增函数.
其中正确的命题序号为
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若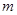 、
、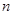 为两条不重合的直线,
为两条不重合的直线, 、
、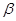 为两个不重合的平面,给出下列命题
为两个不重合的平面,给出下列命题
①若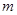 、
、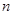 都平行于平面
都平行于平面 ,则
,则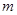 、
、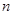 一定不是相交直线;②若
一定不是相交直线;②若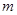 、
、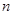 为都垂直于平面
为都垂直于平面 ,则
,则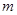 、
、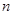 一定是平行直线;③已知
一定是平行直线;③已知 、
、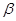 互相垂直,
互相垂直,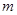 、
、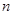 互相垂直,若
互相垂直,若 ;④
;④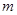 、
、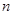 在平面
在平面 内的射影互相垂直,则
内的射影互相垂直,则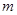 、
、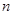 互相垂直。其中的假命题的序号是 .
互相垂直。其中的假命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知命题p:函数f(x)=x2+ax-2在[-1,1]内有且仅有一个零点.命题q:x2+3(a+1)x+2≤0在区间[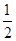 ,
,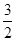 ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com