
给出下列命题:
①函数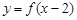 与函数
与函数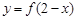 的图象关于
的图象关于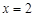 对称
对称
②函数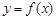 导函数为
导函数为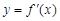 ,若
,若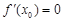 ,则
,则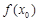 必为函数
必为函数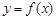 的极值.
的极值.
③函数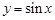 在一象限单调递增
在一象限单调递增
④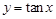 在其定义域内为单调增函数.
在其定义域内为单调增函数.
其中正确的命题序号为
①
解析试题分析:对于①函数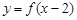 表示的是将y=f(x)右移2个范围得到,而函数
表示的是将y=f(x)右移2个范围得到,而函数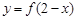 的图象是将f(x)关于y轴对称,再向右移2个单位,因此可知其图像关于
的图象是将f(x)关于y轴对称,再向右移2个单位,因此可知其图像关于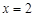 对称,成立。
对称,成立。
对于②函数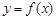 导函数为
导函数为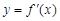 ,若
,若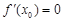 ,则
,则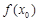 必为函数
必为函数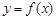 的极值.比如二次函数y=x3,在x=0处不是极值点,但是导数为零的点。故错误。
的极值.比如二次函数y=x3,在x=0处不是极值点,但是导数为零的点。故错误。
对于③函数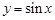 在一象限单调递增,不成立因为角不在一个单调区间内,因为有周期性,错误。
在一象限单调递增,不成立因为角不在一个单调区间内,因为有周期性,错误。
对于④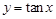 在其定义域内为单调增函数.应该是在每一个区间内递增,不满足单调性定义,错误。故填写①
在其定义域内为单调增函数.应该是在每一个区间内递增,不满足单调性定义,错误。故填写①
考点:本题主要是考查函数图像的变换,以及导数为零点与函数在该点是否取得极值扽问题的运用。
点评:解决该试题的关键是理解单调性和图像的对称性的概念,并能利用条件逐一的加以判定,得到结论。


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
下列叙述正确的序号是 。
(1)对于定义在R上的函数 ,若
,若 ,则函数
,则函数 不是奇函数;
不是奇函数;
(2) 定义在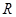 上的函数
上的函数 ,在区间
,在区间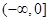 上是单调增函数,在区间
上是单调增函数,在区间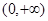 上也是单调增函数,则函数
上也是单调增函数,则函数 在
在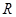 上是单调增函数;
上是单调增函数;
(3) 已知函数的解析式为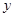 =
=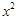 ,它的值域为
,它的值域为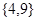 ,那么这样的函数有9个;
,那么这样的函数有9个;
(4)对于任意的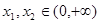 ,若函数
,若函数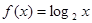 ,则
,则
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出以下五个命题:
① ,若
,若 ,则
,则 或
或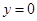 的否命题是假命题;
的否命题是假命题;
②函数 的最小值为2;
的最小值为2;
③若函数 的图象关于点(1,0)对称,则
的图象关于点(1,0)对称,则 的值为-3;
的值为-3;
④若 ,则函数
,则函数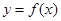 是以4为周期的周期函数;
是以4为周期的周期函数;
⑤若(1+x)10 =a0+a1x+a2x2 +… +a10x10,则a0+a1 +2a2+3a3 +… +10a10=10×29.
其中真命题的序号是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知定义域为 的函数
的函数 满足:①对任意
满足:①对任意 ,恒有
,恒有 成立;当
成立;当 时,
时,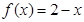 。给出如下结论:
。给出如下结论:
①对任意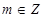 ,有
,有 ;②函数
;②函数 的值域为
的值域为 ;③存在
;③存在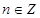 ,使得
,使得 ;④“函数
;④“函数 在区间
在区间 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在 ,使得
,使得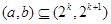 ”。其中所有正确结论的序号是 。
”。其中所有正确结论的序号是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com