
【题目】如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如图,以C为原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系.
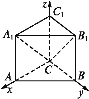
(1)求平面A1B1C的法向量;
(2)求直线AC与平面A1B1C夹角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)v=(x0,y0,z0)为平面A1B1C的法向量,则v·![]() =x0+2z0=0,v·
=x0+2z0=0,v·![]() =y0+2z0=0,解方程组即得平面A1B1C的法向量.(2)利用向量法求直线AC与平面A1B1C夹角的正弦值.
=y0+2z0=0,解方程组即得平面A1B1C的法向量.(2)利用向量法求直线AC与平面A1B1C夹角的正弦值.
(1)由题意可知C(0,0,0),A1(1,0,2),B1(0,1,2),故![]() =(1,0,2),
=(1,0,2),![]() =(0,1,2),
=(0,1,2),
设v=(x0,y0,z0)为平面A1B1C的法向量,则
v·![]() =(x0,y0,z0)(1,0,2)=x0+2z0=0,
=(x0,y0,z0)(1,0,2)=x0+2z0=0,
v·![]() =(x0,y0,z0)(0,1,2)=y0+2z0=0,
=(x0,y0,z0)(0,1,2)=y0+2z0=0,
即![]() 令z0=1,则v=(-2,-2,1).
令z0=1,则v=(-2,-2,1).
(2)设直线AC与平面A1B1C夹角为θ,而![]() =(1,0,0),
=(1,0,0),
所以直线AC与平面A1B1C夹角的正弦值sinθ
=![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数![]() 满足
满足![]() ,且在[0,1)上单调递减,若方程
,且在[0,1)上单调递减,若方程![]() 在[0,1)上有实数根,则方程
在[0,1)上有实数根,则方程![]() 在区间[-1,7]上所有实根之和是
在区间[-1,7]上所有实根之和是
A. 12 B. 14 C. 6 D. 7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为15.
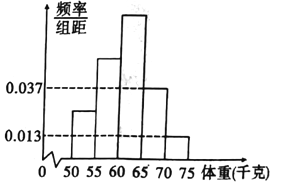
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设![]() 表示体重超过65公斤的学生人数,求
表示体重超过65公斤的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球.
(Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X,求随机变量X的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy 中,曲线C1的参数方程为:![]() (
(![]() ),M是
),M是![]() 上的动点,P点满足
上的动点,P点满足![]() ,P点的轨迹为曲线.
,P点的轨迹为曲线.![]()
(1)求![]() 的参数方程;
的参数方程;
(2)在以O为极点,x 轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为A,与
的异于极点的交点为A,与![]() 的异于极点的交点为B,求
的异于极点的交点为B,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,远离烟草,珍惜生命。据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() ,若将
,若将![]() 沿
沿![]() 折起,得到几何体
折起,得到几何体![]() .
.
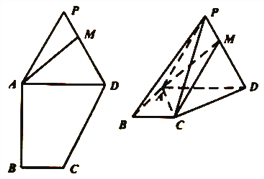
(1)试问:直线![]() 与平面
与平面![]() 是否有公共点?并说明理由;
是否有公共点?并说明理由;
(2)若![]() ,且平面
,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com