
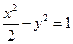 的两个焦点F1,F2的距离之和为定值,
的两个焦点F1,F2的距离之和为定值,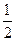 .
.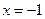 平分?若存在,求出直线l的斜率k的取值范围,若不存在说明理由.
平分?若存在,求出直线l的斜率k的取值范围,若不存在说明理由.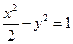 ,
,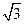 .设|PF1|+|PF2|=2a(常数
.设|PF1|+|PF2|=2a(常数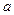 >0),------2分
>0),------2分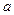 >2c=2
>2c=2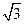 ,∴
,∴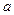 >
>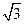
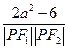 -1
-1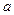 2,
2,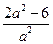 -1,----------4分
-1,----------4分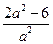 -1=-
-1=-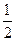 ,解得a2=4,
,解得a2=4,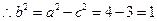
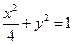 ------------6分
------------6分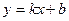 ------------7分
------------7分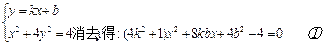
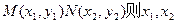
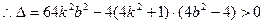
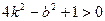 ②------------9分
②------------9分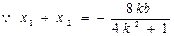 且MN被直线x=-1平分
且MN被直线x=-1平分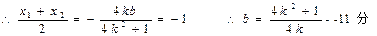
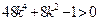 ,解得
,解得 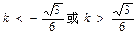
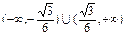


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源:不详 题型:单选题
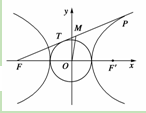
| A.|MO|-|MT|>b-a | B.|MO|-|MT|=b-a |
| C.|MO|-|MT|<b-a | D.不确定 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
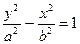 (a>0,b>0)的上、下顶点分别为A、B,一个焦点为F(0,c)(c>0),两准线间的距离为1,|AF|、|AB|、|BF|成等差数列.
(a>0,b>0)的上、下顶点分别为A、B,一个焦点为F(0,c)(c>0),两准线间的距离为1,|AF|、|AB|、|BF|成等差数列. N两点,如果
N两点,如果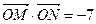 ,求△MBN的面积.
,求△MBN的面积.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.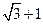 | B.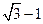 | C.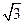 | D.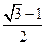 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
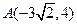 ,它的渐进线方程为
,它的渐进线方程为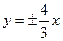
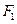 和
和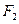 分别是双曲线的左、右焦点,点
分别是双曲线的左、右焦点,点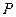 在双曲线上,且
在双曲线上,且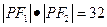
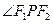 的大小。
的大小。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com