
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 15 | 45 | |
| 无意愿生二胎 | 25 | ||
| 总计 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
分析 (1)由已知可得表格,利用K2计算公式即可得出.
(2))由题意可得,一名男公务员要生二胎意愿的概率为$\frac{30}{30+20}$=$\frac{3}{5}$,无意愿的概率为$\frac{20}{30+20}$$\frac{2}{5}$,记事件A:这三人中至少有一人要生二胎,且各人意愿相互独立.利用P(A)=1-P$(\overline{A})$即可得出.
(3)X可能的取值为0,1,2.利用P(X=k)=$\frac{{∁}_{13}^{2-k}{∁}_{2}^{k}}{{∁}_{15}^{2}}$,即可得出.
解答 解:(1)
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | 45 |
| 无意愿生二胎 | 20 | 25 | 45 |
| 总计 | 50 | 40 | 90 |
| X | 0 | 1 | 2 |
| P | $\frac{26}{35}$ | $\frac{26}{105}$ | $\frac{1}{105}$ |
点评 本题考查了“独立性检验原理”、相互对立事件的概率计算公式、超几何分布列的性质及其数学期望计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 8$\sqrt{5}$ | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $2\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
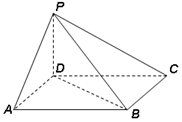 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
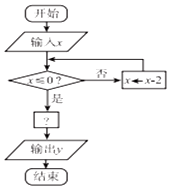 如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )| A. | y=2x+1 | B. | y=3-x | C. | y=|x| | D. | y=log${\;}_{\frac{1}{3}}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com