
【题目】已知函数f(x)=ex﹣1﹣x.
(1)若存在x∈[﹣1,ln ![]() ],满足a﹣ex+1+x<0成立,求实数a的取值范围.
],满足a﹣ex+1+x<0成立,求实数a的取值范围.
(2)当x≥0时,f(x)≥(t﹣1)x恒成立,求实数t的取值范围.
【答案】
(1)解:a﹣ex+1+x<0,
∴a<ex﹣1﹣x,
∴a<f(x),f'(x)=ex﹣1=0,
∴x=0,
∴f(x)在(﹣∞,0)上递减,在(0,+∞)上递增,
x∈[﹣1,ln ![]() ],故最大值应在端点处,
],故最大值应在端点处,
∵f(﹣1)= ![]() ,f(ln
,f(ln ![]() )=
)= ![]() ﹣1﹣ln
﹣1﹣ln ![]() <
< ![]() ,
,
∴a< ![]()
(2)解:当x≥0时,f(x)≥(t﹣1)x恒成立,
∴ex﹣1﹣x≥(t﹣1)x,
∴ex﹣1﹣tx≥0恒成立,
令g(x)=ex﹣1﹣tx,g'(x)=ex﹣t,
若t≤1,则当x≥0时,g'(x)>0,且g(0)=0,
∴当x≥0时,g(x)≥0恒成立,
∴f(x)≥(t﹣1)x恒成立,
若t>1,则当x∈(0,lnt)时,g'(x)<0,g(x)递减,g(0)=0,
∴当x∈(0,lnt)时,g(x)<0.
故不复合题意,
故t的范围为t≤1
【解析】(1)不等式可整理为a<ex﹣1﹣x,只需求出右式在区间内的最大值即可;(2)不等式整理为ex﹣1﹣tx≥0恒成立,构造函数g(x)=ex﹣1﹣tx,求出导函数g'(x)=ex﹣t,对t分类,通过单调性得出t的范围.


科目:高中数学 来源: 题型:
【题目】如图,点P在△ABC内,AB=CP=2,BC=3,∠P+∠B=π,记∠B=α. 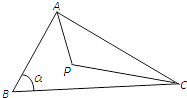
(1)试用α表示AP的长;
(2)求四边形ABCP的面积的最大值,并写出此时α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y= ![]() 的定义域是( )
的定义域是( )
A.[﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() ]
]
B.(﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() )??
)??
C.[﹣2,﹣1)∪(1,2]
D.(﹣2,﹣1)∪(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sin2x,2cos2x﹣1),
=(sin2x,2cos2x﹣1), ![]() =(sinθ,cosθ)(0<θ<π),函数f(x)=
=(sinθ,cosθ)(0<θ<π),函数f(x)= ![]()
![]() 的图象经过点(
的图象经过点( ![]() ,1).
,1).
(1)求θ及f(x)的最小正周期;
(2)当x∈ ![]() 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x)若同时满足:①存在M>0,使得对任意的x1 , x2∈D,都有|f(x1)﹣f(x2)|<M;②f(x)的图象存在对称中心.则称f(x)为“P﹣函数”.
已知函数f1(x)= ![]() 和f2(x)=lg(
和f2(x)=lg( ![]() ﹣x),则以下结论一定正确的是( )
﹣x),则以下结论一定正确的是( )
A.f1(x)和 f2(x)都是P﹣函数
B.f1(x)是P﹣函数,f2(x)不是P﹣函数
C.f1(x)不是P﹣函数,f2(x)是P﹣函数
D.f1(x)和 f2(x)都不是P﹣函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人发现,多看电视容易使人变冷漠,如表是一个调查机构对此现象的调查结果:
冷漠 | 不冷漠 | 总计 | |
多看电视 | 68 | 42 | 110 |
少看电视 | 20 | 38 | 58 |
总计 | 88 | 80 | 168 |
P(K2≥k) | 0.025 | 0.010 | 0.005 | 0.001 |
k | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() ≈11.377,下列说法正确的是( )
≈11.377,下列说法正确的是( )
A.大约有99.9%的把握认为“多看电视与人变冷漠”有关系
B.大约有99.9%的把握认为“多看电视与人变冷漠”没有关系
C.某人爱看电视,则他变冷漠的可能性为99.9%
D.爱看电视的人中大约有99.9%会变冷漠
查看答案和解析>>
科目:高中数学 来源: 题型:
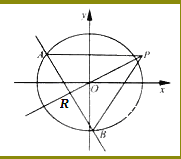
【题目】如图,椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() .不过原点O的直线
.不过原点O的直线![]() 与C相交于A,B两点,且线段AB被直线OP平分.
与C相交于A,B两点,且线段AB被直线OP平分.
(1)求椭圆C的方程;
(2)求![]() ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+bx﹣alnx.
(1)若x=2是函数f(x)的极值点,1和x0是函数f(x)的两个不同零点,且x0∈(n,n+1),n∈N,求n.
(2)若对任意b∈[﹣2,﹣1],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com