
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
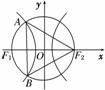
如图所示,F1,F2是双曲线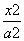 -
-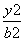 =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点分别为A,B,且△F2AB是等边三角形,则双曲线的离心率为( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点分别为A,B,且△F2AB是等边三角形,则双曲线的离心率为( )
A.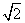 +1 B.
+1 B.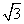 +1 C.
+1 C. 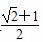 D.
D. 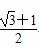
查看答案和解析>>
科目:高中数学 来源: 题型:
由①y=2x+5是一次函数;②y=2x+5的图像是一条直线;③一次函数的图像是一条直线.写一个“三段论”形式的正确推理,则作为大前提、小前提和结论的分别是( )
A.②①③ B.③①②
C.①②③ D.②③①
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a=3,b=-9时,若函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
在对数函数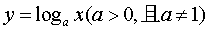 中,下列描述正确的是( )
中,下列描述正确的是( )
①定义域是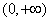 、值域是R ②图像必过点(1,0).
、值域是R ②图像必过点(1,0).
③当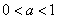 时,在
时,在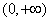 上是减函数;当
上是减函数;当 时,在
时,在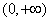 上是增函数.
上是增函数.
④对数函数既不是奇函数,也不是偶函数.
A. ①② B. ②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线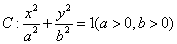 的离心率为
的离心率为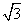 ,焦点到渐近线的距离为
,焦点到渐近线的距离为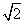
(1)求双曲线C的方程;
(2)已知直线 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆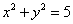 上,求
上,求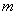 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com