
分析 (1)求出以PC为直径的圆的方程,结合已知圆的方程,由圆系方程可求得两圆公共弦所在直线方程;
(2)设出M,Q的坐标,利用中点坐标公式把Q的坐标用M的坐标表示,代入已知圆的方程得答案.
解答 解:(1)圆C:(x-1)2+y2=1的圆心坐标为C(1,0),半径为1,
则PC的中点坐标为N(2,$\frac{1}{2}$),|PC|=$\sqrt{(3-1)^{2}+(1-0)^{2}}=\sqrt{5}$,
∴以N为圆心,PC为直径的圆的方程为$(x-2)^{2}+(y-\frac{1}{2})^{2}=\frac{5}{4}$,
由(x-1)2+y2=1,得x2+y2-2x=0 ①,
由$(x-2)^{2}+(y-\frac{1}{2})^{2}=\frac{5}{4}$,得x2+y2-4x-y+3=0 ②,
①-②得:2x+y-3=0.
∴直线AB的方程为2x+y-3=0;
(2)设M(x,y),Q(x1,y1),
则$\left\{\begin{array}{l}{2x={x}_{1}+3}\\{2y={y}_{1}+1}\end{array}\right.$,∴$\left\{\begin{array}{l}{{x}_{1}=2x-3}\\{{y}_{1}=2y-1}\end{array}\right.$,即Q(2x-3,2y-1),
代入圆C:(x-1)2+y2=1得:(2x-4)2+(2y-1)2=1,
即$(x-2)^{2}+(y-\frac{1}{2})^{2}=\frac{1}{4}$.
∴PQ的中点M的轨迹方程是$(x-2)^{2}+(y-\frac{1}{2})^{2}=\frac{1}{4}$.
点评 本题考查轨迹方程得求法,训练了代入法求曲线的轨迹方程,特别是(1)的求解,灵活运用圆系方程求出两圆公共弦所在直线方程,解法灵活,起到事半功倍的效果,是中档题.


科目:高中数学 来源: 题型:解答题
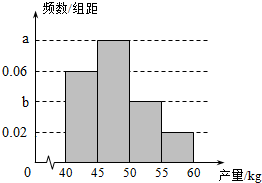 果农种了一片果树,收获时,果农随机随机选取果树20株作为样本.测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60],进行分组,得到频率分布直方图如图,已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.
果农种了一片果树,收获时,果农随机随机选取果树20株作为样本.测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60],进行分组,得到频率分布直方图如图,已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.| 产量 | (40,45] | (45,50] | (50,55] | (55,60] |
| 价格(百元/棵) | 1 | 2 | 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 45 | ||
| 乙班 | 20 | ||
| 合计 | 30 | 105 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com