
【题目】如图,已知PA垂直于矩形ABCD所在的平面,M、N分别为AB、PC的中点,且![]() .
.

(1)求证:![]() 平面PAD;
平面PAD;
(2)求证:![]() 面PCD;
面PCD;
(3)若![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)答案见解析;(2)答案见解析;(3)![]() .
.
【解析】
(1)取CD中点![]() ,连结M
,连结M![]() 、N
、N![]() ,然后可证明平面
,然后可证明平面![]() 平面PAD,进而可得
平面PAD,进而可得![]() 平面PAD;(2)建立空间直角坐标系,利用空间向量可得证得
平面PAD;(2)建立空间直角坐标系,利用空间向量可得证得![]() ,进而得到结论成立;(3)结合题意求出平面MPC和平面MCD的法向量,先求出两向量的夹角的余弦值,然后可得所求二面角的正弦值.
,进而得到结论成立;(3)结合题意求出平面MPC和平面MCD的法向量,先求出两向量的夹角的余弦值,然后可得所求二面角的正弦值.
证明:(1)取CD中点![]() ,连结M
,连结M![]() 、N
、N![]() ,
,
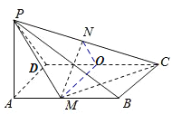
∵N为PC的中点,
∴![]() ,
,
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() .
.
又![]() ,
,
∴平面![]() 平面PAD.
平面PAD.
∵![]() 平面MNO,
平面MNO,
∴![]() 平面PAD.
平面PAD.
(2)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,如下图所示.
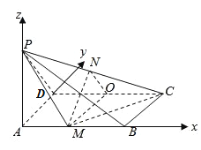
设![]() ,
,![]() ,
,
则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() b,
b,![]() ,
,![]() ,
,![]() b,
b,![]() ,
,
∴![]() ,
,![]() b,
b,![]() ,
,![]() b,
b,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
又![]() ,
,
∴![]() 平面PCD.
平面PCD.
(3)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,如图所示.
设![]() ,则
,则![]() ,
,
则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,
∴![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,
设平面MPC的法向量![]() y,
y,![]() ,
,
则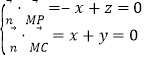 ,取
,取![]() ,得
,得![]() .
.
由题意得平面MCD的法向量![]() 0,
0,![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
∴![]() ,
,
∴二面角![]() 的正弦值为
的正弦值为![]() .
.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,当直线
两点,当直线![]() 与
与![]() 轴平行时,直线
轴平行时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得直线
,使得直线![]() 变化时,总有
变化时,总有![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x+1|+|x﹣3|
(1)求函数f(x)的最小值;
(2)若{x|f(x)≤t2﹣3t}∩{x|﹣2≤x≤0}≠.求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,离心率为
中,离心率为![]() 的椭圆
的椭圆![]() 的左顶点为
的左顶点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() ,
, ![]() 两点.若直线
两点.若直线![]() 斜率为
斜率为 ![]() 时,
时, ![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试问以![]() 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线![]() 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)的定义域是![]() ,对任意
,对任意![]()
当![]() 时,
时,![]() .关于函数
.关于函数![]() 给出下列四个命题:
给出下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 是周期函数;
是周期函数;
③函数![]() 的全部零点为
的全部零点为![]() ;
;
④当![]() 时,函数
时,函数![]() 的图象与函数
的图象与函数![]() 的图象有且只有三个公共点.
的图象有且只有三个公共点.
其中真命题的个数为 .
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是椭圆 ![]() 的左、右焦点F1 , F2关于直线x+y﹣2=0的对称点是圆C的一条直径的两个端点.
的左、右焦点F1 , F2关于直线x+y﹣2=0的对称点是圆C的一条直径的两个端点.
(1)求圆C的方程;
(2)设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a,b.当ab最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S﹣ABCD中,底面ABCD为平行四边形,侧面SBC⊥面ABCD,已知∠ABC=45°,AB=2,BC=2 ![]() ,SB=SC=
,SB=SC= ![]() .
. 
(1)设平面SCD与平面SAB的交线为l,求证:l∥AB;
(2)求证:SA⊥BC;
(3)求直线SD与面SAB所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com