
分析 由题意画出图形.
(1)直接利用数量积公式得答案;
(2)把$\overrightarrow{BC}$用基底$\overrightarrow{AB}、\overrightarrow{AC}$表示,展开后结合(1)得答案;
(3)把$\overrightarrow{AM}$用基底$\overrightarrow{AB}、\overrightarrow{AC}$表示,展开后结合(1)得答案.
解答 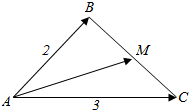 解:如图,$|\overrightarrow{AB}|=2$,$|\overrightarrow{AC}|=3$,∠A=45°,M为BC边上的中点,
解:如图,$|\overrightarrow{AB}|=2$,$|\overrightarrow{AC}|=3$,∠A=45°,M为BC边上的中点,
(1)$\overrightarrow{AB}$•$\overrightarrow{AC}$=$|\overrightarrow{AB}|•|\overrightarrow{AC}|cos45°$=2×$3×\frac{\sqrt{2}}{2}$=$3\sqrt{2}$;
(2)$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\overrightarrow{AB}•(\overrightarrow{AC}-\overrightarrow{AB})=\overrightarrow{AB}•\overrightarrow{AC}-|\overrightarrow{AB}{|}^{2}$=$3\sqrt{2}-4$;
(3)$\overrightarrow{AB}$•$\overrightarrow{AM}$=$\overrightarrow{AB}•\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{2}|\overrightarrow{AB}{|}^{2}+\frac{1}{2}\overrightarrow{AB}•\overrightarrow{AC}$=$2+\frac{3\sqrt{2}}{2}$.
点评 本题考查平面向量的数量积运算,考查了平面向量基本定理,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
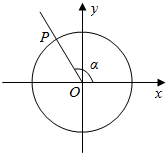 如图,已知角α的终边在第二象限,且与单位圆交于点P(m,$\frac{\sqrt{15}}{4}$).
如图,已知角α的终边在第二象限,且与单位圆交于点P(m,$\frac{\sqrt{15}}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | $\frac{b}{a}$<1 | C. | lg(a-b)>lg$\frac{1}{a-b}$ | D. | 4-a<4-b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -98 | D. | 98 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(k)=0 | B. | f(k)<0 | C. | f(k)>0 | D. | f(k)的符号不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com